Advertisements
Advertisements
प्रश्न
एक त्रिभुज ABC खींचिए, जिसमें AB = 4 cm, BC = 6 cm और AC = 9 cm है। इस ΔABC के समरूप, स्केल गुणक `3/2` के एक त्रिभुज की रचना कीजिए। रचना का औचित्य दीजिए क्या दोनों त्रिभुज सर्वांगसम हैं? ध्यान दीजिए कि यहाँ दोनों त्रिभुजों में तीनों कोण और दो भुजाएँ बराबर हैं।
Advertisements
उत्तर
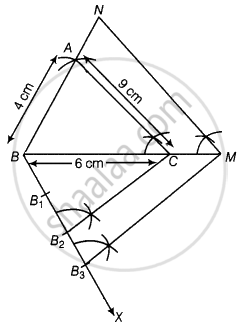
निर्माण के चरण:
- एक रेखाखंड BC = 6 cm खींचिए।
- B और C को केंद्र मानकर 4 cm और 9 cm त्रिज्या के दो चाप खींचिए जो एक दूसरे को A पर काटते हैं।
- BA और CA को जोड़ें, ΔABC अभीष्ट त्रिभुज है।
- B से न्यूनकोण बनाते हुए कोई भी किरण BX नीचे की ओर खींचिए।
- BX पर तीन बिंदु B1, B2, B3 अंकित करें, जैसे कि BB1 = B1B2 = B2B3।
- B2C को जोड़ें और B3 से ड्रा करें B3M || B2C विस्तारित रेखा खंड BC को M पर प्रतिच्छेद करता है।
- बिंदु M से, खींचिए MN || CA विस्तारित रेखा खंड BA को N पर प्रतिच्छेद करता है।
फिर, ΔNBM आवश्यक त्रिभुज है जिसकी भुजाएँ ΔABC की संगत भुजाओं के `3/2` के बराबर हैं।
औचित्य:
यहाँ, B3M || B2C
∴ `"BC"/"CM" = 2/1`
अब, `"BM"/"BC" = ("BC" + "CM")/"BC"`
= `1 + "CM"/"BC"`
= `1 + 1/2`
= `3/2`
साथ ही, MN || CA
∴ ΔABC ∼ ΔNBM
इसलिए, `"NB"/"AB" = "NM"/"AC" = "BM"/"BC" = 3/2`
दोनों त्रिभुज सर्वांगसम नहीं हैं, क्योंकि यदि दो त्रिभुज सर्वांगसम हैं, तो उनका आकार और आकार समान होता है। यहां तीनों कोण तो एक जैसे हैं लेकिन तीन भुजाएं एक जैसी नहीं हैं यानी एक भुजा अलग-अलग है।
APPEARS IN
संबंधित प्रश्न
4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर उसके समरूप एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ पहले त्रिभुज की संगत भुजाओं की `2/3` हों। निर्माण का औचित्य बताइए।
एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी और ∠ABC = 60 हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ΔABC की संगत भुजाओं की `3/4` गुनी हों। औचित्य बताइए
एक त्रिभुज ABC बनाइए, जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ΔABC की संगत भुजाओं की `4/3` गुनी हों। और औचित्य बताइए
एक समकोण त्रिभुज बनाइए, जिसकी भुजाएँ (कर्ण के अलावा) 4 सेमी और 3 सेमी लंबी हों। एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए गए त्रिभुज की संगत भुजाओं की `5/3` गुनी हों। निर्माण का औचित्य बताइए।
एक रेखाखंड AB को 5 : 6 के अनुपात में विभाजित करने के लिए, एक किरण AX खींचिए ताकि ∠BAX एक न्यून कोण हो, फिर किरण BY किरण AX के समांतर विपरीत दिशा में खींचिए। इसके बाद AX और BY किरणों पर क्रमशः समान दूरियों पर बिंदु A1, A2, A3, ... और B1, B2, B3, ... अंकित किये जाएँ। फिर जिन बिंदुओं को मिलाया जाता है वे हैं।
एक दिये हुए त्रिभुज ABC के समरूप एक ऐसा त्रिभुज बनाने के लिए जिसकी भुजाएँ ΔABC की संगत भुजाओं का `8/5` हों, पहले एक किरण BX ऐसी खींचिए कि ∠CBX एक न्यून कोण हो और X भुजा BC के सापेक्ष A के विपरीत ओर हो। किरण BX पर अब समान दूरियों पर अंकित किये जाने वाले बिंदुओं की न्यूनतम संख्या है।
ज्यामितीय रचना से, एक दिये हुए रेखाखंड को `sqrt(3) : 1/sqrt(3)` के अनुपात में विभाजित किया जा सकता है।
एक त्रिभुज ABC खींचिए, जिसमें BC = 6 cm, CA = 5 cm और AB = 4 cm है। इस त्रिभुज के समरूप और स्केल गुणक `5/3` के एक त्रिभुज की रचना कीजिए।
एक समद्विबाहु त्रिभुज ABC खींचिए, जिसमें AB = AC = 6 cm और BC = 5 cm है। ΔABC के समरूप, एक त्रिभुज PQR की रचना कीजिए, जिसमें PQ = 8 cm हो।अपनी रचना का औचित्य भी दीजिए।
एक त्रिभुज ABC खींचिए, जिसमें AB = 5 cm, BC = 6 cm और ∠ABC = 60° है। ΔABC के समरूप, स्केल गुणक `5/7` के एक त्रिभुज की रचना कीजिए। रचना का औचित्य दीजिए।
