Advertisements
Advertisements
प्रश्न
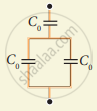
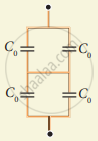
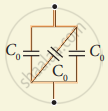
Find the capacitances of the capacitors shown in figure . The plate area is Aand the separation between the plates is d. Different dielectric slabs in a particular part of the figure are of the same thickness and the entire gap between the plates is filled with the dielectric slabs.
उत्तर
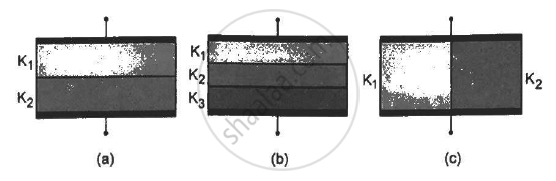
The two parts of the capacitor are in series with capacitances C1 and C2.
Here,
`C_1 = (K_1∈_0A)/(d/2) and C_2 = (K_2∈_0A)/(d/2)`
⇒ `C_1 = (2K_1∈_0A)/d and C_2 = (2K_2∈_0A)/d`
Because they are in series, the net capacitance is calculated as :
`C = (C_1 xx C_2)/(C_1+C_2)`
= `((2K_1∈_0A)/d xx (2K_2∈_0A)/d)/((2K_1∈_0A)/d xx (2K_2∈_0A)/d)`
= `(2K_1K_2∈_0A)/(d(K_1+K_2)`
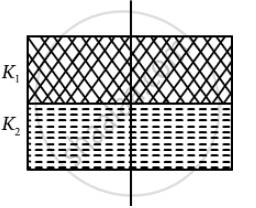
(b) Here, the capacitor has three parts. These can be taken in series.
Now ,
`C_1 = (K_1∈_0A)/((d/3)) = (3K_1∈_0A)/d`
`C_2 = (3K_2∈_0A)/d`
`C_3 = (3K_3∈_0A)/d`
Thus, the net capacitance is calculated as :
`C = (C_1 xx C_2 xx C_2)/(C_1C_2+C_2C_3+C_3C_1)`
= `((3K_1∈_0A)/d xx (3K_2∈_0A)/d xx (3K_3∈_0A)/d)/((3K_1∈_0A)/d xx (3K_2∈_0A)/d xx (3K_2∈_0A)/d xx (3K_3∈_0A)/d xx (3K_3∈_0A)/d xx (3K_1∈_0A)/d)`
= `(3 ∈_0 K_1K_2K_3)/(d(K_1K_2+K_2K_3+K_3K_1)`
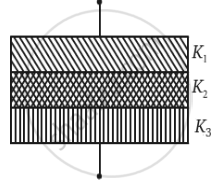
(c)
Here ,
`C_1 = (K_1∈_0A/2)/d = (K_1∈_0A)/(2d)`
`C_2 = (K_2∈_0A)/(2d)`
These two parts are in parallel.
`therefore C = C_1 + C_2`
= `(∈_0A)/(2d)(K_1+K_2)`
APPEARS IN
संबंधित प्रश्न
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (a) The electric field between the plates of the capacitor Justify your answer by writing the necessary expressions.
Define capacitor reactance. Write its S.I units.
A parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
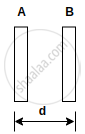
A capacitor has capacitance C. Is this information sufficient to know what maximum charge the capacitor can contain? If yes, what is this charges? If no, what other information is needed?
Following operations can be performed on a capacitor:
X − connect the capacitor to a battery of emf ε.
Y − disconnect the battery.
Z − reconnect the battery with polarity reversed.
W − insert a dielectric slab in the capacitor.
(a) In XYZ (perform X, then Y, then Z) the stored electric energy remains unchanged and no thermal energy is developed.
(b) The charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
(c) The electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
(d) The electric field in the capacitor after the action XW is the same as that after WX.
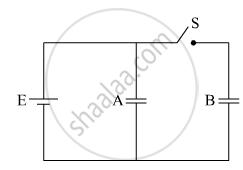
Find the charge supplied by the battery in the arrangement shown in figure.
A cylindrical capacitor is constructed using two coaxial cylinders of the same length 10 cm and of radii 2 mm and 4 mm. (a) Calculate the capacitance. (b) Another capacitor of the same length is constructed with cylinders of radii 4 mm and 8 mm. Calculate the capacitance.
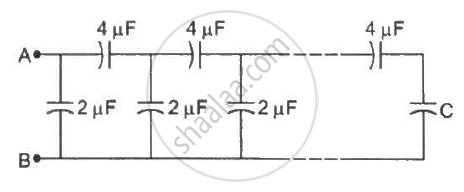
A finite ladder is constructed by connecting several sections of 2 µF, 4 µF capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance C. What value should be chosen for C, such that the equivalent capacitance of the ladder between the points A and B becomes independent of the number of sections in between?
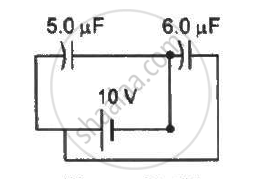
A 5⋅0 µF capacitor is charged to 12 V. The positive plate of this capacitor is now connected to the negative terminal of a 12 V battery and vice versa. Calculate the heat developed in the connecting wires.
The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
A parallel-plate capacitor of capacitance 5 µF is connected to a battery of emf 6 V. The separation between the plates is 2 mm. (a) Find the charge on the positive plate. (b) Find the electric field between the plates. (c) A dielectric slab of thickness 1 mm and dielectric constant 5 is inserted into the gap to occupy the lower half of it. Find the capacitance of the new combination. (d) How much charge has flown through the battery after the slab is inserted?
You are provided with 8 μF capacitors. Show with the help of a diagram how you will arrange minimum number of them to get a resultant capacitance of 20 μF.
Calculate the resultant capacitances for each of the following combinations of capacitors.
A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of resulting system ______.
Three capacitors 2µF, 3µF, and 6µF are joined in series with each other. The equivalent capacitance is ____________.
The capacitance of a parallel plate capacitor is 60 µF. If the distance between the plates is tripled and area doubled then new capacitance will be ______.
Consider two conducting spheres of radii R1 and R2 with R1 > R2. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.
Two plates A and B of a parallel plate capacitor are arranged in such a way, that the area of each plate is S = 5 × 10-3 m 2 and distance between them is d = 8.85 mm. Plate A has a positive charge q1 = 10-10 C and Plate B has charge q2 = + 2 × 10-10 C. Then the charge induced on the plate B due to the plate A be - (....... × 10-11 )C
A capacitor of capacity 2 µF is charged to a potential difference of 12 V. It is then connected across an inductor of inductance 0.6 mH. The current in the circuit at a time when the potential difference across the capacitor is 6.0 V is ______ × 10-1A.