Advertisements
Advertisements
प्रश्न
Following operations can be performed on a capacitor:
X − connect the capacitor to a battery of emf ε.
Y − disconnect the battery.
Z − reconnect the battery with polarity reversed.
W − insert a dielectric slab in the capacitor.
(a) In XYZ (perform X, then Y, then Z) the stored electric energy remains unchanged and no thermal energy is developed.
(b) The charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
(c) The electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
(d) The electric field in the capacitor after the action XW is the same as that after WX.
उत्तर
(b) The charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
(c) The electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
(d) The electric field in the capacitor after the action XW is the same as that after WX.
Justification of option (b)
If the potential is held constant, that is, the battery remains attached to the circuit, then the charge on the capacitor increases by a factor of K on inserting a dielectric of a dielectric constant K between the plates of the capacitor.
Mathematically,
q = Kq0
Here, q0 and q are the charges without dielectric and with dielectric, respectively.
The amount of charge stored does not depend upon the polarity of the plates.
Thus, the charge appearing on the capacitor is greater after the action XWY than after the action XYZ.
Justification of option (c)
Since the battery is disconnected before inserting a dielectric, the amount of charge remains constant, that is,q = q0, because after the battery is disconnected, the capacitor gets no source to store charge from. In other words, the capacitor is now an isolated system where the amount of charge is conserved and so is the energy U as `1/2q∈` . Hence, inserting a dielectric after disconnecting the battery will not bring any change in the amount of charge stored in the capacitor. So, the energy stored in the capacitor will also not change after the action XYW.
However, during the action WXY, the amount of charge that will get stored in the capacitor will get increased by a factor of K, as the battery is disconnected after inserting a dielectric between the plates of the capacitor and the energy stored will also get multiplied by a factor of K.
Thus, the electric energy stored in the capacitor is greater after the action WXY than after the action XYW.
Justification of option (d)
The electric field between the plates E depends on the potential across the capacitor and the distanced between the plates of the capacitor.
Mathematically,
`E = ∈/d`
In either case, that is, during actions XW and WX, the potential remains the same, that is, ∈. Thus, the electric field E remains the same.
Denial of option (a)
During the action XYZ, the battery has to do extra work equivalent to `1/2CV^2` to change the polarity of the plates of the capacitor. In other words, the total work to be done by the battery will be `1/2CV^2+1/2CV^2` . This extra work done will be dissipated as heat energy. Thus, thermal energy is developed. However, the stored electric energy remains unchanged, that is `1/2CV^2` .
APPEARS IN
संबंधित प्रश्न
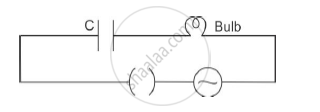
A bulb is connected in series with a variable capacitor and an AC source as shown. What happens to the brightness of the bulb when the key is plugged in and capacitance of the capacitor is gradually reduced?
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (a) The electric field between the plates of the capacitor Justify your answer by writing the necessary expressions.
The capacitance of a capacitor does not depend on
When 1⋅0 × 1012 electrons are transferred from one conductor to another, a potential difference of 10 V appears between the conductors. Calculate the capacitance of the two-conductor system.
Each capacitor shown in figure has a capacitance of 5⋅0 µF. The emf of the battery is 50 V. How much charge will flow through AB if the switch S is closed?
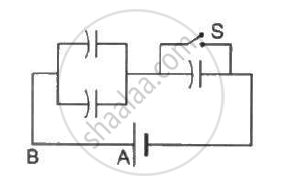
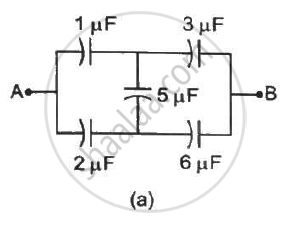
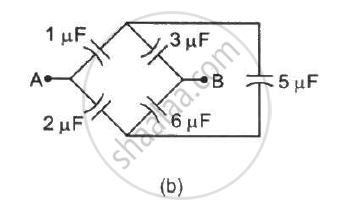
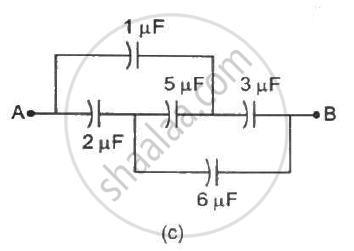
Convince yourself that parts (a), (b) and (c) figure are identical. Find the capacitance between the points A and B of the assembly.
A 5⋅0 µF capacitor is charged to 12 V. The positive plate of this capacitor is now connected to the negative terminal of a 12 V battery and vice versa. Calculate the heat developed in the connecting wires.
A parallel-plate capacitor has plate area 100 cm2 and plate separation 1⋅0 cm. A glass plate (dielectric constant 6⋅0) of thickness 6⋅0 mm and an ebonite plate (dielectric constant 4⋅0) are inserted one over the other to fill the space between the plates of the capacitor. Find the new capacitance.
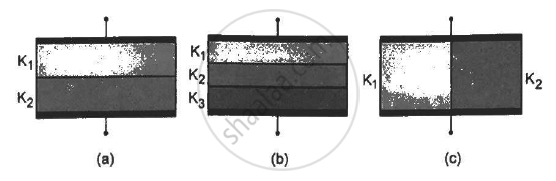
Find the capacitances of the capacitors shown in figure . The plate area is Aand the separation between the plates is d. Different dielectric slabs in a particular part of the figure are of the same thickness and the entire gap between the plates is filled with the dielectric slabs.
An air-filled parallel-plate capacitor is to be constructed which can store 12 µC of charge when operated at 1200 V. What can be the minimum plate area of the capacitor? The dielectric strength of air is `3 xx 10^6 "Vm"^-1`
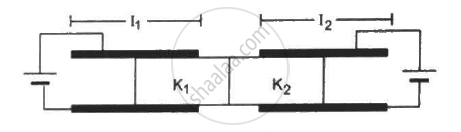
Figure shows two parallel plate capacitors with fixed plates and connected to two batteries. The separation between the plates is the same for the two capacitors. The plates are rectangular in shape with width b and lengths l1 and l2. The left half of the dielectric slab has a dielectric constant K1 and the right half K2. Neglecting any friction, find the ration of the emf of the left battery to that of the right battery for which the dielectric slab may remain in equilibrium.
You are provided with 8 μF capacitors. Show with the help of a diagram how you will arrange minimum number of them to get a resultant capacitance of 20 μF.
A parallel plate capacitor stores a charge Q at a voltage V. Suppose the area of the parallel plate capacitor and the distance between the plates are each doubled then which is the quantity that will change?
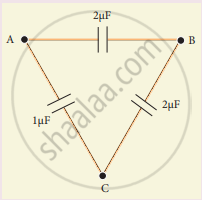
Three capacitors are connected in a triangle as shown in the figure. The equivalent capacitance between points A and C is ______.
Derive the expression for resultant capacitance, when the capacitor is connected in series.
During a thunder storm, the movement of water molecules within the clouds creates friction, partially causing the bottom part of the clouds to become negatively charged. This implies that the bottom of the cloud and the ground act as a parallel plate capacitor. If the electric field between the cloud and ground exceeds the dielectric breakdown of the air (3 × 106 Vm–1), lightning will occur.

- If the bottom part of the cloud is 1000 m above the ground, determine the electric potential difference that exists between the cloud and ground.
- In a typical lightning phenomenon, around 25 C of electrons are transferred from cloud to ground. How much electrostatic potential energy is transferred to the ground?
- Charge on each capacitor remains same and equals to the main charge supplied by the battery.
- Potential difference and energy distribute in the reverse ratio of capacitance.
- Effective capacitance is even les than the least of teh individual capacitances.
Dielectric constant for a metal is ______.
A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε = αU where α = 2V–1. A similar capacitor with no dielectric is charged to U0 = 78V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
For changing the capacitance of a given parallel plate capacitor, a dielectric material of dielectric constant K is used, which has the same area as the plates of the capacitor.
The thickness of the dielectric slab is `3/4`d, where 'd' is the separation between the plate of the parallel plate capacitor.
The new capacitance (C') in terms of the original capacitance (C0) is given by the following relation:
