Advertisements
Advertisements
प्रश्न
When 1⋅0 × 1012 electrons are transferred from one conductor to another, a potential difference of 10 V appears between the conductors. Calculate the capacitance of the two-conductor system.
उत्तर
As 1.0 × 1012 electrons are transferred from one conductor to another, the conductor to which the electrons are transferred becomes negatively charged and the other conductor becomes positively charged.
Now ,
Magnitude of the net charge on each conductor, `Q = (1.0 xx 10^12) xx (1.6 xx 10^-19) C = 1.6 xx 10^-7 C`
Magnitude of the potential difference between the conductors, V = 10 V
The capacitance C is the ratio of the magnitude of the charge on either conductor to the magnitude of the potential difference between the conductors.
`C = Q/V`
⇒ `C = (1.6 xx 10^-7)/10 = 1.6 xx 10^-8 F`
Hence, the value of the capacitance of the given two conductor systems is `1.6 xx 10^-8 F` .
APPEARS IN
संबंधित प्रश्न
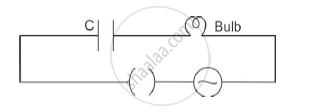
A bulb is connected in series with a variable capacitor and an AC source as shown. What happens to the brightness of the bulb when the key is plugged in and capacitance of the capacitor is gradually reduced?
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (a) The electric field between the plates of the capacitor Justify your answer by writing the necessary expressions.
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 µC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor.
(b) What is the potential of the inner sphere?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm. Explain why the latter is much smaller.
A parallel-plate capacitor has plate area 25⋅0 cm2 and a separation of 2⋅00 mm between the plates. The capacitor is connected to a battery of 12⋅0 V. (a) Find the charge on the capacitor. (b) The plate separation is decreased to 1⋅00 mm. Find the extra charge given by the battery to the positive plate.
Find the capacitance of the combination shown in figure between A and B.

A parallel-plate capacitor of capacitance 5 µF is connected to a battery of emf 6 V. The separation between the plates is 2 mm. (a) Find the charge on the positive plate. (b) Find the electric field between the plates. (c) A dielectric slab of thickness 1 mm and dielectric constant 5 is inserted into the gap to occupy the lower half of it. Find the capacitance of the new combination. (d) How much charge has flown through the battery after the slab is inserted?
A parallel-plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. Find the work done on the system in the process of inserting the slab.
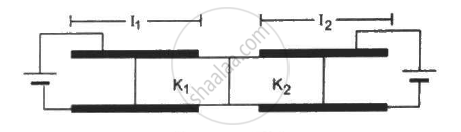
Figure shows two parallel plate capacitors with fixed plates and connected to two batteries. The separation between the plates is the same for the two capacitors. The plates are rectangular in shape with width b and lengths l1 and l2. The left half of the dielectric slab has a dielectric constant K1 and the right half K2. Neglecting any friction, find the ration of the emf of the left battery to that of the right battery for which the dielectric slab may remain in equilibrium.
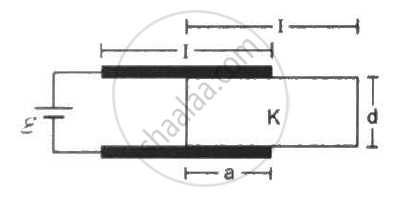
Consider the situation shown in figure. The plates of the capacitor have plate area A and are clamped in the laboratory. The dielectric slab is released from rest with a length a inside the capacitor. Neglecting any effect of friction or gravity, show that the slab will execute periodic motion and find its time period.
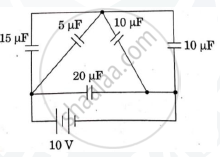
The figure show a network of five capacitors connected to a 10V battery. Calculate the charge acquired by the 5μF capacitor.
Obtain an expression for equivalent capacitance when three capacitors C1, C2 and C3 are connected in series.
If the voltage applied on a capacitor is increased from V to 2V, choose the correct conclusion.
Obtain the expression for energy stored in the parallel plate capacitor.
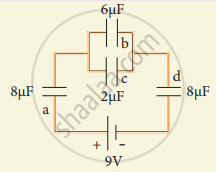
For the given capacitor configuration
- Find the charges on each capacitor
- potential difference across them
- energy stored in each capacitor.
- Charge on each capacitor remains same and equals to the main charge supplied by the battery.
- Potential difference and energy distribute in the reverse ratio of capacitance.
- Effective capacitance is even les than the least of teh individual capacitances.
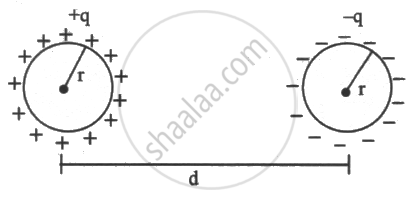
Two similar conducting spheres having charge+ q and -q are placed at 'd' seperation from each other in air. The radius of each ball is r and the separation between their centre is d (d >> r). Calculate the capacitance of the two ball system ______.
A capacitor of capacity 2 µF is charged to a potential difference of 12 V. It is then connected across an inductor of inductance 0.6 mH. The current in the circuit at a time when the potential difference across the capacitor is 6.0 V is ______ × 10-1A.
A capacitor has charge 50 µC. When the gap between the plate is filled with glass wool, then 120 µC charge flows through the battery to capacitor. The dielectric constant of glass wool is ______.
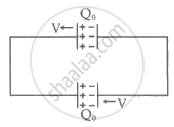
Two identical capacitors are connected as shown and have an initial charge of Q0. The separation between the plates of each capacitor is d0. Suddenly the left plate of the upper capacitor and right plate of the lower capacitor start moving with speed v towards the left while the other plate of each capacitor remains fixed. `("given" (Q_0V)/(2d_0) = 10 A)`. The value of current in the circuit is ______ A.