Advertisements
Advertisements
प्रश्न
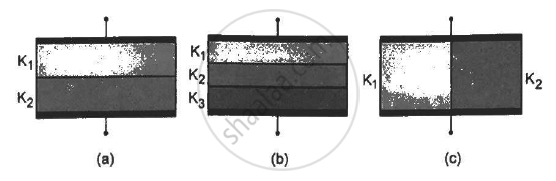
Find the capacitances of the capacitors shown in figure . The plate area is Aand the separation between the plates is d. Different dielectric slabs in a particular part of the figure are of the same thickness and the entire gap between the plates is filled with the dielectric slabs.
उत्तर
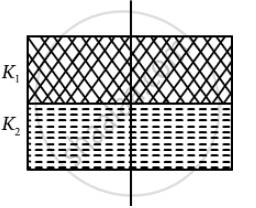
The two parts of the capacitor are in series with capacitances C1 and C2.
Here,
`C_1 = (K_1∈_0A)/(d/2) and C_2 = (K_2∈_0A)/(d/2)`
⇒ `C_1 = (2K_1∈_0A)/d and C_2 = (2K_2∈_0A)/d`
Because they are in series, the net capacitance is calculated as :
`C = (C_1 xx C_2)/(C_1+C_2)`
= `((2K_1∈_0A)/d xx (2K_2∈_0A)/d)/((2K_1∈_0A)/d xx (2K_2∈_0A)/d)`
= `(2K_1K_2∈_0A)/(d(K_1+K_2)`
(b) Here, the capacitor has three parts. These can be taken in series.
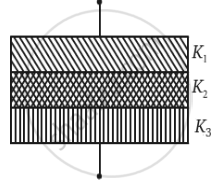
Now ,
`C_1 = (K_1∈_0A)/((d/3)) = (3K_1∈_0A)/d`
`C_2 = (3K_2∈_0A)/d`
`C_3 = (3K_3∈_0A)/d`
Thus, the net capacitance is calculated as :
`C = (C_1 xx C_2 xx C_2)/(C_1C_2+C_2C_3+C_3C_1)`
= `((3K_1∈_0A)/d xx (3K_2∈_0A)/d xx (3K_3∈_0A)/d)/((3K_1∈_0A)/d xx (3K_2∈_0A)/d xx (3K_2∈_0A)/d xx (3K_3∈_0A)/d xx (3K_3∈_0A)/d xx (3K_1∈_0A)/d)`
= `(3 ∈_0 K_1K_2K_3)/(d(K_1K_2+K_2K_3+K_3K_1)`
(c)
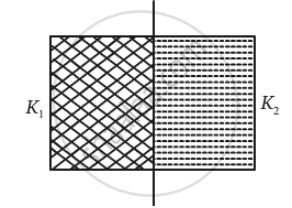
Here ,
`C_1 = (K_1∈_0A/2)/d = (K_1∈_0A)/(2d)`
`C_2 = (K_2∈_0A)/(2d)`
These two parts are in parallel.
`therefore C = C_1 + C_2`
= `(∈_0A)/(2d)(K_1+K_2)`
APPEARS IN
संबंधित प्रश्न
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (a) The electric field between the plates of the capacitor Justify your answer by writing the necessary expressions.
A parallel plate capacitor of capacitance C is charged to a potential V. It is then connected to another uncharged capacitor having the same capacitance. Find out the ratio of the energy stored in the combined system to that stored initially in the single capacitor.
(i) Find equivalent capacitance between A and B in the combination given below. Each capacitor is of 2 µF capacitance.
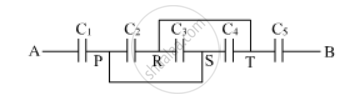
(ii) If a dc source of 7 V is connected across AB, how much charge is drawn from the source and what is the energy stored in the network?
Two identical capacitors of 12 pF each are connected in series across a battery of 50 V. How much electrostatic energy is stored in the combination? If these were connected in parallel across the same battery, how much energy will be stored in the combination now?
Also find the charge drawn from the battery in each case.
A capacitor of capacitance ‘C’ is being charged by connecting it across a dc source along with an ammeter. Will the ammeter show a momentary deflection during the process of charging? If so, how would you explain this momentary deflection and the resulting continuity of current in the circuit? Write the expression for the current inside the capacitor.
Two metal spheres of capacitance C1 and C2 carry some charges. They are put in contact and then separated. The final charges Q1 and Q2 on them will satisfy
The capacitance of a capacitor does not depend on
Suppose, one wishes to construct a 1⋅0 farad capacitor using circular discs. If the separation between the discs be kept at 1⋅0 mm, what would be the radius of the discs?
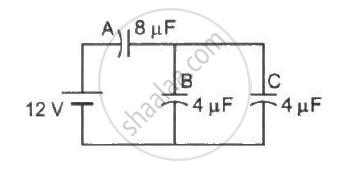
Find the charge appearing on each of the three capacitors shown in figure .
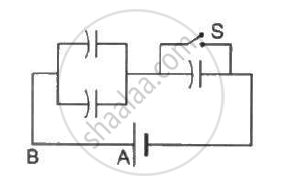
Each capacitor shown in figure has a capacitance of 5⋅0 µF. The emf of the battery is 50 V. How much charge will flow through AB if the switch S is closed?
A parallel-plate capacitor of capacitance 5 µF is connected to a battery of emf 6 V. The separation between the plates is 2 mm. (a) Find the charge on the positive plate. (b) Find the electric field between the plates. (c) A dielectric slab of thickness 1 mm and dielectric constant 5 is inserted into the gap to occupy the lower half of it. Find the capacitance of the new combination. (d) How much charge has flown through the battery after the slab is inserted?
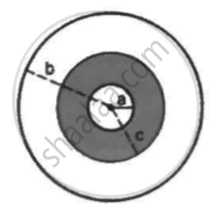
A sphercial capacitor is made of two conducting spherical shells of radii a and b. The space between the shells is filled with a dielectric of dielectric constant K up to a radius c as shown in figure . Calculate the capacitance.
Three capacitors C1 = 3μF, C2 = 6μF, and C3 = 10μF are connected to a 50 V battery as shown in Figure below:

Calculate:
(i) The equivalent capacitance of the circuit between points A and B.
(ii) The charge on C1.
- Charge on each capacitor remains same and equals to the main charge supplied by the battery.
- Potential difference and energy distribute in the reverse ratio of capacitance.
- Effective capacitance is even les than the least of teh individual capacitances.
The work done in placing a charge of 8 × 10–18 coulomb on a condenser of capacity 100 micro-farad is ______.
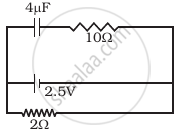
A capacitor of 4 µ F is connected as shown in the circuit (Figure). The internal resistance of the battery is 0.5 Ω. The amount of charge on the capacitor plates will be ______.
A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε = αU where α = 2V–1. A similar capacitor with no dielectric is charged to U0 = 78V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
Two plates A and B of a parallel plate capacitor are arranged in such a way, that the area of each plate is S = 5 × 10-3 m 2 and distance between them is d = 8.85 mm. Plate A has a positive charge q1 = 10-10 C and Plate B has charge q2 = + 2 × 10-10 C. Then the charge induced on the plate B due to the plate A be - (....... × 10-11 )C