Advertisements
Advertisements
प्रश्न
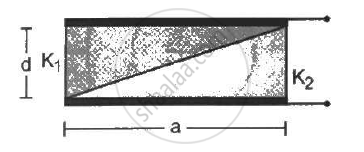
A capacitor is formed by two square metal-plates of edge a, separated by a distance d. Dielectrics of dielectric constant K1 and K2 are filled in the gap as shown in figure . Find the capacitance.
उत्तर

Let us consider an elemental capacitor of width dx at a distance x from the left end of the capacitor. It has two capacitive elements of dielectric constants K1 and K2 with plate separations (x tan θ) and (d − x tan θ) in series, respectively. The areas of the plates of the capacitors are adx.
The capacitances of the capacitive elements of the elemental capacitor are :
`dC_1 = (∈_0K_2(adx))/(x tan θ) , dC_2 = (∈_0K_1(adx))/(d - x tan θ)`
The net capacitance of the elemental capacitor is given by
`1/(dC)= 1/(dC_1) + 1/(dC_2)`
`1/(dC) = (x tanθ)/(∈_0K_2(adx)) + (d-x tanθ)/(∈_0K_1(adx))`
`⇒ dC = (∈_0K_1K_2(adx))/(K_1 x tanθ + K_2(d-x tanθ)`
Thus, integrating the above expression to calculate the net capacitance
`C = ∫_0^a dC = ∫_0^a (∈_0K_1K_2adx)/(K_1x tanθ+ K_2(d-x tanθ)`
`⇒ C = ∈_0K_1K_2a ∫_0^a (dx)/(K_2d + x tanθ(K_1 - K_2)`
`⇒ C = (∈_0K_1K_2a)/(tanθ(K_1 - K_2))[log_e[K_2d + x tanθ(K_1 - K_2) ]]_0^a`
`⇒ C = (∈_0K_1K_2a)/(tan θ(K_1 - K_2)) [ log_e[K_2d + a tan θ(K_1 - K_2)] - log_e K_2d]`
As we know that `tan θ = d/a` substituting in the expression for capacitance C.
Now,
`⇒ C = (∈_0K_1K_2a)/(d/a xx (K_1 - K_2) )[ log_e[K_2d + a xx d/a(K_1 - K_2)] - log_e K_2d]`
`⇒ C = (∈_0K_1K_2a)/(d/a xx (K_1 - K_2) )[ log_e K_1d - log_e K_2d ]`
`⇒ C = (∈_0K_1K_2a^2)/(d(K_1 - K_2)) [log_e (K_1/K_2)]`
APPEARS IN
संबंधित प्रश्न
A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 360 μC. When potential across the capacitor is reduced by 120 V, the charge stored in it becomes 120 μC.
Calculate:
(i) The potential V and the unknown capacitance C.
(ii) What will be the charge stored in the capacitor, if the voltage applied had increased by 120 V?
A capacitor of capacitance ‘C’ is being charged by connecting it across a dc source along with an ammeter. Will the ammeter show a momentary deflection during the process of charging? If so, how would you explain this momentary deflection and the resulting continuity of current in the circuit? Write the expression for the current inside the capacitor.
A parallel-plate capacitor has plate area 25⋅0 cm2 and a separation of 2⋅00 mm between the plates. The capacitor is connected to a battery of 12⋅0 V. (a) Find the charge on the capacitor. (b) The plate separation is decreased to 1⋅00 mm. Find the extra charge given by the battery to the positive plate.
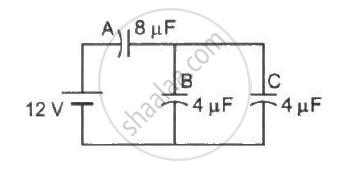
Find the charge appearing on each of the three capacitors shown in figure .
The outer cylinders of two cylindrical capacitors of capacitance 2⋅2 µF each, are kept in contact and the inner cylinders are connected through a wire. A battery of emf 10 V is connected as shown in figure . Find the total charge supplied by the battery to the inner cylinders.

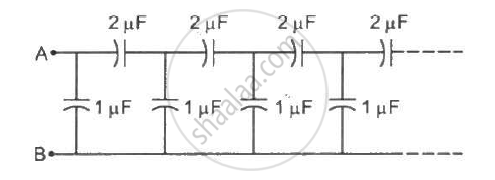
Each of the capacitors shown in figure has a capacitance of 2 µF. find the equivalent capacitance of the assembly between the points A and B. Suppose, a battery of emf 60 volts is connected between A and B. Find the potential difference appearing on the individual capacitors.
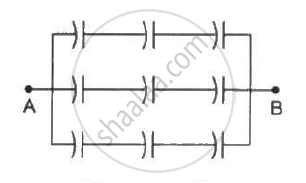
Find the equivalent capacitance of the infinite ladder shown in figure between the points A and B.
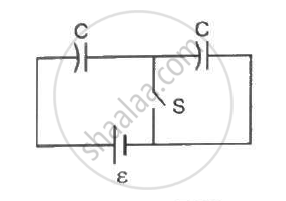
Consider the situation shown in the figure. The switch S is open for a long time and then closed. (a) Find the charge flown through the battery when the switch S is closed. (b) Find the work done by the battery.(c) Find the change in energy stored in the capacitors.(d) Find the heat developed in the system.
A 5⋅0 µF capacitor is charged to 12 V. The positive plate of this capacitor is now connected to the negative terminal of a 12 V battery and vice versa. Calculate the heat developed in the connecting wires.
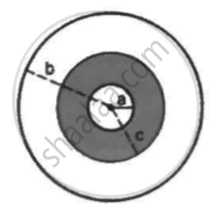
A sphercial capacitor is made of two conducting spherical shells of radii a and b. The space between the shells is filled with a dielectric of dielectric constant K up to a radius c as shown in figure . Calculate the capacitance.
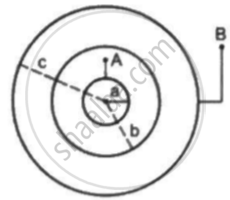
Consider an assembly of three conducting concentric spherical shell of radii a, b and c as shown in figure Find the capacitance of the assembly between the points Aand B.

Suppose the space between the two inner shells is filled with a dielectric of dielectric constant K. Find the capacitance of the system between A and B.
If the voltage applied on a capacitor is increased from V to 2V, choose the correct conclusion.
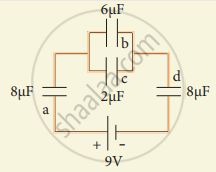
For the given capacitor configuration
- Find the charges on each capacitor
- potential difference across them
- energy stored in each capacitor.
The positive terminal of 12 V battery is connected to the ground. Then the negative terminal will be at ______.
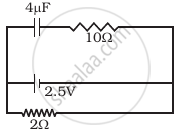
A capacitor of 4 µ F is connected as shown in the circuit (Figure). The internal resistance of the battery is 0.5 Ω. The amount of charge on the capacitor plates will be ______.
A leaky parallel plate capacitor is filled completely with a material having dielectric constant K = 5 and electric conductivity σ = 7.4 × 10-12 Ω-1 m-1. If the charge on the plate at the instant t = 0 is q = 8.85 µC, then the leakage current at the instant t = 12 s is ______ × 10-1 µA.
A capacitor with capacitance 5µF is charged to 5 µC. If the plates are pulled apart to reduce the capacitance to 2 µF, how much work is done?
