Advertisements
Advertisements
प्रश्न
Find the equation of a line passing through the intersection of x + 2y + 1= 0 and 2x - 3y = 12 and perpendicular to the line 2x + 3y = 9
उत्तर
x + 2y + 1 = 0.............(1)
2x - 3y = 12...........(2)
(1) can be written as 2x + 4y = -2....(3)
(2) can be rewritten as 2x - 3y = 12........(4)
subtracting (4) from (3) we get
y = -2
x = 3
i.e (3,-2)
Point of intersection of (1) and (2) is (3,-2)
Slope of 2x + 3y = 9 is `(-2)/3`
Slope of required line is `3/2`
equation of required lineis `("y" - "y"_1)/("x" - "x"_1)` = m
`("y" + 2)/("x" - 3) = 2/3`
⇒ #x - 9 = 2y + 4
⇒ 3x - 2y = 13
APPEARS IN
संबंधित प्रश्न
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(0, 5)
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(–5, 0)
Find the equation of a line whose : y-intercept = −1 and inclination = 45°
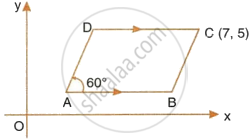
The following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, ∠A = 60° and vertex C = (7, 5). Find the equations of BC and CD.
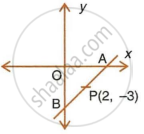
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
Find if the following points lie on the given line or not:
(2,4) on the line y = 2x - 1
L is a point on the line segment PQ dividing it in the ratio 1 : 3. If the coordinates of P and Q are (3, 7) and ( 11,-5) respectively, find if L lies on the line 2x + 5y = 20.
Find the equation of a line whose slope and y-intercept are m = -3, c = -1
Find the equation of a line passing through (8,3) and making an angle of 45° with the positive direction of the y-axis.
Find the equation of a line passing through (3, – 2) and perpendicular to the line.
x - 3y + 5 = 0.
