Advertisements
Advertisements
प्रश्न
Find the equation of a line passing through the intersection of x + 3y = 6 and 2x - 3y = 12 and parallel to the line 5x + 2y = 10
उत्तर
x + 3y = 6...........(1)
2x - 3y = 12..........(2)
Adding (1) and (2), we get
3x = 18
⇒ x = 6
And y = 0
Point of intersection of given line is (6,0)
Slope of 5x + 2y = 10 is `(-5)/2`
Slope of required line is `(-5)/2`
Equation of required line is `("y" - "y"_1)/("x" - "x"_1)` = slope
`("y" - 0)/("x" - 6) = (-5)/2`
⇒ -5x + 30 = 2y
⇒ 5x + 2y - 30 = 0
APPEARS IN
संबंधित प्रश्न
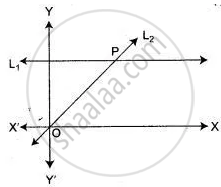
Given the equation of line L, is y = 4.
(1) Write the slope of line L2, if L2, is the bisector of angle O.
(2) Write the co–ordinates of point P.
(3) Find the equation of L2.
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(0, 5)
Find the equation of a line which passes through (5, 4) and makes an angle of 60° with the positive direction of the x-axis.
A, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) respectively. Find the equation of the line through A and perpendicular to BC.
Find the equation of the line with x-intercept 5 and a point on it (–3, 2).
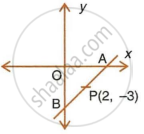
A and B are two points on the x-axis and y-axis respectively. P(2, −3) is the mid point of AB. Find the
- co-ordinates of A and B
- slope of line AB
- equation of line AB.
The vertices of a ΔABC are A(3, 8), B(–1, 2) and C(6, –6). Find:
(i) Slope of BC
(ii) Equation of a line perpendicular to BC and passing through A.
Find if the following points lie on the given line or not:
(2,4) on the line y = 2x - 1
Find the value of a line parallel to the following line:
x = `"y"/2` - 5
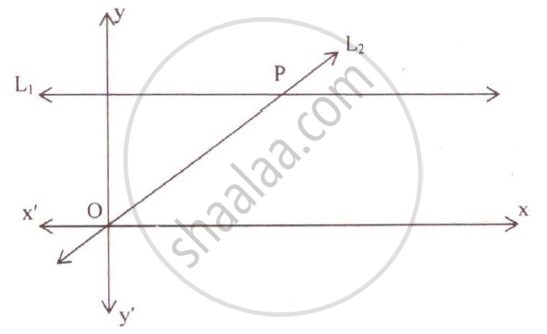
Given equation of line L1 is y = 4.
(i) Write the slope of line, if L2 is the bisector of angle O.
(ii) Write the coordinates of point P.
(iii) Find the equation of L2