Advertisements
Advertisements
प्रश्न
Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
उत्तर
Let a and b be the intercepts made on the axes by the line passing through P(2, 2).
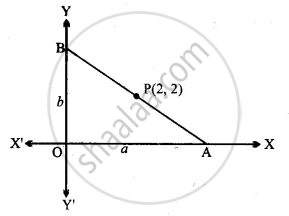
equation of line in intercept form
`"x"/"a" + "y"/"b" = 1`
This line passes through P(2, 2).
∴ `2/"a" + 2/"b" = 1` ..........(i)
It is given that the sum of the segments is 9.
∴ a + b = 9
b = 9 – a
Putting the value of b in (i),
`2/"a" + 2/(9 -"a") = 1`
or 2(9 – a) + 2a = a (9 – a)
18 – 2a + 2a = 9a – a2
or a2 – 9a + 18 = 0
or (a – 6)(a – 3) = 0
a = 6, 3
b = 3, 6
When a = 6 and b = 3, then the required equation of the line is
`"x"/6 + "y"/3 = 1`
or 3x + 6y = 18
or x + 2y = 6
When a = 3 and b = 6, then the required equation of the line is,
`"x"/3 + "y"/6 = 1`
2x + y - 6 = 0
or x + 2y - 6 = 0
APPEARS IN
संबंधित प्रश्न
Find the equation of the line which satisfy the given condition:
Write the equations for the x and y-axes.
Find the equation of the line which satisfy the given condition:
Passing through the point (–4, 3) with slope `1/2`.
Find the equation of the line which satisfy the given condition:
Passing though `(2, 2sqrt3)` and is inclined with the x-axis at an angle of 75°.
Find the equation of the line which satisfy the given condition:
Intersects the x-axis at a distance of 3 units to the left of origin with slope –2.
Find the equation of the line which satisfy the given condition:
Intersects the y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Find the equation of the line which satisfy the given condition:
Passing through the points (–1, 1) and (2, –4).
Find the equation of the line which is at a perpendicular distance of 5 units from the origin and the angle made by the perpendicular with the positive x-axis is 30°
Find the equation of the line which satisfy the given condition:
The vertices of ΔPQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.
Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).
Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
Find equation of the line through the point (0, 2) making an angle `(2pi)/3` with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?
P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is `x/a + y/b = 2`
Point R (h, k) divides a line segment between the axes in the ratio 1:2. Find equation of the line.
Find the values of q and p, if the equation x cos q + y sinq = p is the normal form of the line `sqrt3 x` + y + 2 = 0.
Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
Classify the following pair of line as coincident, parallel or intersecting:
2x + y − 1 = 0 and 3x + 2y + 5 = 0
Classify the following pair of line as coincident, parallel or intersecting:
x − y = 0 and 3x − 3y + 5 = 0]
Find the equation to the straight line parallel to 3x − 4y + 6 = 0 and passing through the middle point of the join of points (2, 3) and (4, −1).
Prove that the lines 2x − 3y + 1 = 0, x + y = 3, 2x − 3y = 2 and x + y = 4 form a parallelogram.
Find the angle between the lines x = a and by + c = 0..
Prove that the area of the parallelogram formed by the lines a1x + b1y + c1 = 0, a1x + b1y+ d1 = 0, a2x + b2y + c2 = 0, a2x + b2y + d2 = 0 is \[\left| \frac{\left( d_1 - c_1 \right)\left( d_2 - c_2 \right)}{a_1 b_2 - a_2 b_1} \right|\] sq. units.
Deduce the condition for these lines to form a rhombus.
Show that the diagonals of the parallelogram whose sides are lx + my + n = 0, lx + my + n' = 0, mx + ly + n = 0 and mx + ly + n' = 0 include an angle π/2.
Show that the point (3, −5) lies between the parallel lines 2x + 3y − 7 = 0 and 2x + 3y + 12 = 0 and find the equation of lines through (3, −5) cutting the above lines at an angle of 45°.
Three vertices of a parallelogram taken in order are (−1, −6), (2, −5) and (7, 2). The fourth vertex is
Let ABC be a triangle with A(–3, 1) and ∠ACB = θ, 0 < θ < `π/2`. If the equation of the median through B is 2x + y – 3 = 0 and the equation of angle bisector of C is 7x – 4y – 1 = 0, then tan θ is equal to ______.
