Advertisements
Advertisements
प्रश्न
P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is `x/a + y/b = 2`
उत्तर
Let AB be the line segment between the axes and let P (a, b) be its mid-point.
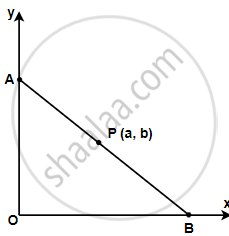
Let the coordinates of A and B be (0, y) and (x, 0) respectively.
Since P (a, b) is the mid-point of AB,
`(0 + x)/2, (y + 0)/2 = (a, b)`
=`(x/2, y/2) = (a, b)`
= `x/2 = a and y/2 = b`
∴ x = 2a and y = 2a
Thus, the respective coordinates of A and B are (0, 2b) and (2a, 0).
The equation of the line passing through points (0, 2b) and (2a, 0) is
`(y - 2b) = ((0 - 2b))/((2a - 0)) (x - 0)`
`y - 2b = (-2b)/(2a) (x)`
a (y - 2b) = -bx
ay - 2ab = bx
i.e. bx + ay = 2ab
On dividing both sides by ab, we obtain
`(bx)/(ab) + (ay)/(ab) + (2ab)/(ab)`
= `x/a + y/b = 2`
Thus, the equation of the line is `x/a + y/b = 2`
APPEARS IN
संबंधित प्रश्न
Find the equation of the line which satisfy the given condition:
Write the equations for the x and y-axes.
Find the equation of the line which satisfy the given condition:
Passing though (0, 0) with slope m.
Find the equation of the line which satisfy the given condition:
Passing though `(2, 2sqrt3)` and is inclined with the x-axis at an angle of 75°.
Find the equation of the line which satisfy the given condition:
Intersects the y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Find the equation of the line which satisfy the given condition:
Passing through the points (–1, 1) and (2, –4).
Find the equation of the line which is at a perpendicular distance of 5 units from the origin and the angle made by the perpendicular with the positive x-axis is 30°
Find the equation of the line which satisfy the given condition:
The vertices of ΔPQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.
The vertices of ΔPQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.
A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1:n. Find the equation of the line.
Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
Find equation of the line through the point (0, 2) making an angle `(2pi)/3` with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L = 125.134 when C = 110, express L in terms of C
The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?
Point R (h, k) divides a line segment between the axes in the ratio 1:2. Find equation of the line.
Find the values of q and p, if the equation x cos q + y sinq = p is the normal form of the line `sqrt3 x` + y + 2 = 0.
Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Classify the following pair of line as coincident, parallel or intersecting:
3x + 2y − 4 = 0 and 6x + 4y − 8 = 0.
Prove that the lines \[\sqrt{3}x + y = 0, \sqrt{3}y + x = 0, \sqrt{3}x + y = 1 \text { and } \sqrt{3}y + x = 1\] form a rhombus.
Find the angle between the lines x = a and by + c = 0..
Find the equation of the line mid-way between the parallel lines 9x + 6y − 7 = 0 and 3x + 2y + 6 = 0.
Prove that the area of the parallelogram formed by the lines a1x + b1y + c1 = 0, a1x + b1y+ d1 = 0, a2x + b2y + c2 = 0, a2x + b2y + d2 = 0 is \[\left| \frac{\left( d_1 - c_1 \right)\left( d_2 - c_2 \right)}{a_1 b_2 - a_2 b_1} \right|\] sq. units.
Deduce the condition for these lines to form a rhombus.
Prove that the area of the parallelogram formed by the lines 3x − 4y + a = 0, 3x − 4y + 3a = 0, 4x − 3y− a = 0 and 4x − 3y − 2a = 0 is \[\frac{2}{7} a^2\] sq. units..
Show that the point (3, −5) lies between the parallel lines 2x + 3y − 7 = 0 and 2x + 3y + 12 = 0 and find the equation of lines through (3, −5) cutting the above lines at an angle of 45°.
Write an equation representing a pair of lines through the point (a, b) and parallel to the coordinate axes.
Let ABC be a triangle with A(–3, 1) and ∠ACB = θ, 0 < θ < `π/2`. If the equation of the median through B is 2x + y – 3 = 0 and the equation of angle bisector of C is 7x – 4y – 1 = 0, then tan θ is equal to ______.
