Advertisements
Advertisements
प्रश्न
Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
उत्तर
Line AB passes through the point P(2, 3) and makes equal intercepts on the coordinate axes.
OA = OB
∠BAO = 45°,
∠BAX = 135°
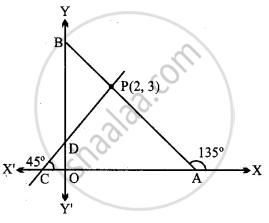
Slope of AB, m = tan 135° = –1
Equation of line, y – y1 = m(x – x1)
Where x1 = 2, Y1 = 3 and m = –1
y – 3 = – (x – 2)
or x + y – 5 = 0
or x + y = 5
APPEARS IN
संबंधित प्रश्न
Find the equation of the line which satisfy the given condition:
Write the equations for the x and y-axes.
Find the equation of the line which satisfy the given condition:
Passing though `(2, 2sqrt3)` and is inclined with the x-axis at an angle of 75°.
Find the equation of the line which satisfy the given condition:
Intersects the x-axis at a distance of 3 units to the left of origin with slope –2.
Find the equation of the line which satisfy the given condition:
Intersects the y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Find the equation of the line which satisfy the given condition:
Passing through the points (–1, 1) and (2, –4).
The vertices of ΔPQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.
Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).
Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
Find equation of the line through the point (0, 2) making an angle `(2pi)/3` with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
The perpendicular from the origin to a line meets it at the point (– 2, 9), find the equation of the line.
The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?
P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is `x/a + y/b = 2`
By using the concept of equation of a line, prove that the three points (3, 0), (–2, –2) and (8, 2) are collinear.
Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
Classify the following pair of line as coincident, parallel or intersecting:
2x + y − 1 = 0 and 3x + 2y + 5 = 0
Classify the following pair of line as coincident, parallel or intersecting:
x − y = 0 and 3x − 3y + 5 = 0]
Prove that the lines 2x − 3y + 1 = 0, x + y = 3, 2x − 3y = 2 and x + y = 4 form a parallelogram.
Find the angle between the lines x = a and by + c = 0..
Find the equation of the line mid-way between the parallel lines 9x + 6y − 7 = 0 and 3x + 2y + 6 = 0.
Prove that the area of the parallelogram formed by the lines 3x − 4y + a = 0, 3x − 4y + 3a = 0, 4x − 3y− a = 0 and 4x − 3y − 2a = 0 is \[\frac{2}{7} a^2\] sq. units..
Show that the diagonals of the parallelogram whose sides are lx + my + n = 0, lx + my + n' = 0, mx + ly + n = 0 and mx + ly + n' = 0 include an angle π/2.
Show that the point (3, −5) lies between the parallel lines 2x + 3y − 7 = 0 and 2x + 3y + 12 = 0 and find the equation of lines through (3, −5) cutting the above lines at an angle of 45°.
Write an equation representing a pair of lines through the point (a, b) and parallel to the coordinate axes.
Three vertices of a parallelogram taken in order are (−1, −6), (2, −5) and (7, 2). The fourth vertex is
