Advertisements
Advertisements
Question
Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
Solution
Line AB passes through the point P(2, 3) and makes equal intercepts on the coordinate axes.
OA = OB
∠BAO = 45°,
∠BAX = 135°
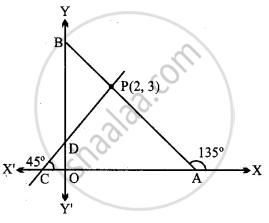
Slope of AB, m = tan 135° = –1
Equation of line, y – y1 = m(x – x1)
Where x1 = 2, Y1 = 3 and m = –1
y – 3 = – (x – 2)
or x + y – 5 = 0
or x + y = 5
APPEARS IN
RELATED QUESTIONS
Find the equation of the line which satisfy the given condition:
Passing through the point (–4, 3) with slope `1/2`.
Find the equation of the line which satisfy the given condition:
Passing though (0, 0) with slope m.
Find the equation of the line which satisfy the given condition:
Passing though `(2, 2sqrt3)` and is inclined with the x-axis at an angle of 75°.
Find the equation of the line which satisfy the given condition:
Intersects the y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Find the equation of the line which satisfy the given condition:
Passing through the points (–1, 1) and (2, –4).
Find the equation of the line which is at a perpendicular distance of 5 units from the origin and the angle made by the perpendicular with the positive x-axis is 30°
A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1:n. Find the equation of the line.
Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L = 125.134 when C = 110, express L in terms of C
P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is `x/a + y/b = 2`
By using the concept of equation of a line, prove that the three points (3, 0), (–2, –2) and (8, 2) are collinear.
Find the values of q and p, if the equation x cos q + y sinq = p is the normal form of the line `sqrt3 x` + y + 2 = 0.
Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
Classify the following pair of line as coincident, parallel or intersecting:
x − y = 0 and 3x − 3y + 5 = 0]
Classify the following pair of line as coincident, parallel or intersecting:
3x + 2y − 4 = 0 and 6x + 4y − 8 = 0.
Prove that the lines \[\sqrt{3}x + y = 0, \sqrt{3}y + x = 0, \sqrt{3}x + y = 1 \text { and } \sqrt{3}y + x = 1\] form a rhombus.
Find the equation to the straight line parallel to 3x − 4y + 6 = 0 and passing through the middle point of the join of points (2, 3) and (4, −1).
Find the angle between the lines x = a and by + c = 0..
Prove that the area of the parallelogram formed by the lines a1x + b1y + c1 = 0, a1x + b1y+ d1 = 0, a2x + b2y + c2 = 0, a2x + b2y + d2 = 0 is \[\left| \frac{\left( d_1 - c_1 \right)\left( d_2 - c_2 \right)}{a_1 b_2 - a_2 b_1} \right|\] sq. units.
Deduce the condition for these lines to form a rhombus.
Prove that the area of the parallelogram formed by the lines 3x − 4y + a = 0, 3x − 4y + 3a = 0, 4x − 3y− a = 0 and 4x − 3y − 2a = 0 is \[\frac{2}{7} a^2\] sq. units..
Show that the point (3, −5) lies between the parallel lines 2x + 3y − 7 = 0 and 2x + 3y + 12 = 0 and find the equation of lines through (3, −5) cutting the above lines at an angle of 45°.
Write an equation representing a pair of lines through the point (a, b) and parallel to the coordinate axes.
Three vertices of a parallelogram taken in order are (−1, −6), (2, −5) and (7, 2). The fourth vertex is
