Advertisements
Advertisements
प्रश्न
Find the equation of the perpendicular drawn from the point P (−1, 3, 2) to the line \[\overrightarrow{r} = \left( 2 \hat{j} + 3 \hat{k} \right) + \lambda\left( 2 \hat{i} + \hat{j} + 3 \hat{k} \right) .\] Also, find the coordinates of the foot of the perpendicular from P.
उत्तर
Let L be the foot of the perpendicular drawn from the point P ( -1, 3, 2) to the line \[\overrightarrow{r} = \left( 2 \hat{j} + 3 \hat{k} \right) + \lambda\left( 2 \hat{i} + \hat{j} + 3 \hat{k} \right) .\]
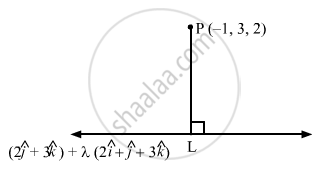
Let the position vector L be \[\overrightarrow{r} = \left( 2 \hat{j} + 3 \hat{k} \right) + \lambda\left( 2 \hat{i} + \hat{j} + 3 \hat{k} \right) = 2\lambda \hat{i} + \left( 2 + \lambda \right) \hat{j} + \left( 3 + 3\lambda \right) \hat{k} \] ...........(1)
Now,
\[\overrightarrow{PL} = \text{ Position vector of L - Position vector of P } \]
\[ \Rightarrow \overrightarrow{PL} = \left\{ 2\lambda \hat{i} + \left( 2 + \lambda \right) \hat{j} + \left( 3 + 3\lambda \right) \hat{k} \right\} - \left( - \hat{i} + 3 \hat{j} + 2 \hat{k} \right)\]
\[ \Rightarrow \overrightarrow{PL} = \left( 2\lambda + 1 \right) \hat{i} + \left( \lambda - 1 \right) \hat{j} + \left( 3\lambda + 1 \right) \hat{k} . . . (2)\]
Since \[\overrightarrow{PL}\] is perpendicular to the given line, which is parallel to \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 3 \hat{k} \]
we have ,
\[\overrightarrow{PL} . \overrightarrow{b} = 0\]
\[ \Rightarrow \left\{ \left( 2\lambda + 1 \right) \hat{i} + \left( \lambda - 1 \right) \hat{j} + \left( 3\lambda + 1 \right) \hat{k} \right\} . \left( 2 \hat{i} + \hat{j} + 3 \hat{k} \right) = 0 \]
\[ \Rightarrow 2\left( 2\lambda + 1 \right) + 1\left( \lambda - 1 \right) + 3\left( 3\lambda + 1 \right) = 0\]
\[ \Rightarrow \lambda = - \frac{2}{7}\]
Substituting \[ \Rightarrow \lambda = - \frac{2}{7}\] in (1),
we get the position vector of L as \[- \frac{4}{7} \hat{i} + \frac{12}{7} \hat{j} + \frac{15}{7} \hat{k} \] So, the coordinates of the foot of the perpendicular from P to the given line is L \[\left( - \frac{4}{7}, \frac{12}{7}, \frac{15}{7} \right)\]
Substituting \[\lambda = - \frac{2}{7}\] in (2), we get \[\overrightarrow{PL} = \frac{3}{7} \hat{i} - \frac{9}{7} \hat{j} + \frac{1}{7} \hat{k} \]
Equation of the perpendicular drawn from P to the given line is
\[\overrightarrow{r} = \text{ Position vector of P } + \lambda\left( \vec{PL} \right)\]
\[ = \left( - \hat{i} + 3 \hat{j} + 2 \hat{k} \right) + \lambda\left( 3 \hat{i} - 9 \hat{j} + \hat{k} \right)\]
APPEARS IN
संबंधित प्रश्न
Find the value of p, so that the lines `l_1:(1-x)/3=(7y-14)/p=(z-3)/2 and l_2=(7-7x)/3p=(y-5)/1=(6-z)/5 ` are perpendicular to each other. Also find the equations of a line passing through a point (3, 2, – 4) and parallel to line l1.
Let `A(bara)` and `B(barb)` be any two points in the space and `R(barr)` be a point on the line segment AB dividing it internally in the ratio m : n, then prove that `bar r=(mbarb+nbara)/(m+n)` . Hence find the position vector of R which divides the line segment joining the points A(1, –2, 1) and B(1, 4, –2) internally in the ratio 2 : 1.
Show that the three lines with direction cosines `12/13, (-3)/13, (-4)/13; 4/13, 12/13, 3/13; 3/13, (-4)/13, 12/13 ` are mutually perpendicular.
Find the direction cosines of the line \[\frac{4 - x}{2} = \frac{y}{6} = \frac{1 - z}{3} .\] Also, reduce it to vector form.
Find the vector equation of the line passing through the point A(1, 2, –1) and parallel to the line 5x – 25 = 14 – 7y = 35z.
Find the equation of a line parallel to x-axis and passing through the origin.
Find the angle between the following pair of line:
\[\overrightarrow{r} = \left( 3 \hat{i} + 2 \hat{j} - 4 \hat{k} \right) + \lambda\left( \hat{i} + 2 \hat{j} + 2 \hat{k} \right) \text{ and } \overrightarrow{r} = \left( 5 \hat{j} - 2 \hat{k} \right) + \mu\left( 3 \hat{i} + 2 \hat{j} + 6 \hat{k} \right)\]
Find the angle between the pairs of lines with direction ratios proportional to 2, 2, 1 and 4, 1, 8 .
Find the angle between two lines, one of which has direction ratios 2, 2, 1 while the other one is obtained by joining the points (3, 1, 4) and (7, 2, 12).
Find the equations of the line passing through the point (−1, 2, 1) and parallel to the line \[\frac{2x - 1}{4} = \frac{3y + 5}{2} = \frac{2 - z}{3} .\]
Show that the lines \[\frac{x - 5}{7} = \frac{y + 2}{- 5} = \frac{z}{1} \text{ and } \frac{x}{1} = \frac{y}{2} = \frac{z}{3}\] are perpendicular to each other.
Find the vector equation of the line passing through the point (2, −1, −1) which is parallel to the line 6x − 2 = 3y + 1 = 2z − 2.
Find the value of λ so that the following lines are perpendicular to each other. \[\frac{x - 5}{5\lambda + 2} = \frac{2 - y}{5} = \frac{1 - z}{- 1}, \frac{x}{1} = \frac{2y + 1}{4\lambda} = \frac{1 - z}{- 3}\]
Prove that the lines through A (0, −1, −1) and B (4, 5, 1) intersects the line through C (3, 9, 4) and D (−4, 4, 4). Also, find their point of intersection.
Find the foot of the perpendicular drawn from the point \[\hat{i} + 6 \hat{j} + 3 \hat{k} \] to the line \[\overrightarrow{r} = \hat{j} + 2 \hat{k} + \lambda\left( \hat{i} + 2 \hat{j} + 3 \hat{k} \right) .\] Also, find the length of the perpendicular
Find the shortest distance between the following pairs of lines whose vector equations are: \[\overrightarrow{r} = \left( \lambda - 1 \right) \hat{i} + \left( \lambda + 1 \right) \hat{j} - \left( 1 + \lambda \right) \hat{k} \text{ and } \overrightarrow{r} = \left( 1 - \mu \right) \hat{i} + \left( 2\mu - 1 \right) \hat{j} + \left( \mu + 2 \right) \hat{k} \]
Find the shortest distance between the following pairs of lines whose vector are: \[\overrightarrow{r} = \left( \hat{i} + \hat{j} \right) + \lambda\left( 2 \hat{i} - \hat{j} + \hat{k} \right) \text{ and } , \overrightarrow{r} = 2 \hat{i} + \hat{j} - \hat{k} + \mu\left( 3 \hat{i} - 5 \hat{j} + 2 \hat{k} \right)\]
Find the shortest distance between the following pairs of lines whose vector equations are: \[\overrightarrow{r} = \left( 8 + 3\lambda \right) \hat{i} - \left( 9 + 16\lambda \right) \hat{j} + \left( 10 + 7\lambda \right) \hat{k} \]\[\overrightarrow{r} = 15 \hat{i} + 29 \hat{j} + 5 \hat{k} + \mu\left( 3 \hat{i} + 8 \hat{j} - 5 \hat{k} \right)\]
Write the vector equations of the following lines and hence determine the distance between them \[\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z + 4}{6} \text{ and } \frac{x - 3}{4} = \frac{y - 3}{6} = \frac{z + 5}{12}\]
Write the cartesian and vector equations of X-axis.
Write the vector equation of a line passing through a point having position vector \[\overrightarrow{\alpha}\] and parallel to vector \[\overrightarrow{\beta}\] .
Write the direction cosines of the line \[\frac{x - 2}{2} = \frac{2y - 5}{- 3}, z = 2 .\]
The equations of a line are given by \[\frac{4 - x}{3} = \frac{y + 3}{3} = \frac{z + 2}{6} .\] Write the direction cosines of a line parallel to this line.
Find the angle between the lines
\[\vec{r} = \left( 2 \hat{i} - 5 \hat{j} + \hat{k} \right) + \lambda\left( 3 \hat{i} + 2 \hat{j} + 6 \hat{k} \right)\] and \[\vec{r} = 7 \hat{i} - 6 \hat{k} + \mu\left( \hat{i} + 2 \hat{j} + 2 \hat{k} \right)\]
If the direction ratios of a line are proportional to 1, −3, 2, then its direction cosines are
The straight line \[\frac{x - 3}{3} = \frac{y - 2}{1} = \frac{z - 1}{0}\] is
Show that the lines \[\frac{5 - x}{- 4} = \frac{y - 7}{4} = \frac{z + 3}{- 5} \text { and } \frac{x - 8}{7} = \frac{2y - 8}{2} = \frac{z - 5}{3}\] are coplanar.
Find the value of p for which the following lines are perpendicular :
`(1-x)/3 = (2y-14)/(2p) = (z-3)/2 ; (1-x)/(3p) = (y-5)/1 = (6-z)/5`
If the lines represented by kx2 − 3xy + 6y2 = 0 are perpendicular to each other, then
Choose correct alternatives:
The difference between the slopes of the lines represented by 3x2 - 4xy + y2 = 0 is 2
The equation 4x2 + 4xy + y2 = 0 represents two ______
If 2x + y = 0 is one of the line represented by 3x2 + kxy + 2y2 = 0 then k = ______
If slopes of lines represented by kx2 - 4xy + y2 = 0 differ by 2, then k = ______
Find the vector equation of a line passing through a point with position vector `2hati - hatj + hatk` and parallel to the line joining the points `-hati + 4hatj + hatk` and `-hati + 2hatj + 2hatk`.
Find the equations of the diagonals of the parallelogram PQRS whose vertices are P(4, 2, – 6), Q(5, – 3, 1), R(12, 4, 5) and S(11, 9, – 2). Use these equations to find the point of intersection of diagonals.
