Advertisements
Advertisements
प्रश्न
Find the lengths of the medians of a ΔABC whose vertices are A(0,-1) , B(2,1) and C (0.3).
उत्तर
The vertices of ABC A(0,-1) , B(2,1) and C (0.3)
Let AD, BE and CF be the medians of Δ ABC.
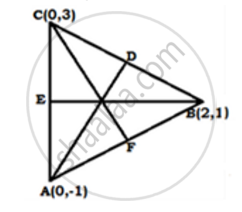
Let D be the midpoint of BC. So, the coordinates of D ar
`D ((2+0)/2 , (1+3)/2) i.e D (2/2 , 4/2) i.e D (1,2)`
Let E be the midpoint of AC. So the coordinate of E are
`E ((0+0)/2 , (-1+3)/2) i.e . E (0/2,0/2) i.e E (0,1) `
Let F be the midpoint of AB. So, the coordinates of F are
` F ((0+2)/2 , (-1+1)/2) i.e F (2/2 , 0/2) i.e F (1,0) `
`AD = sqrt((1-0)^2 +(2-(-1))^2) = sqrt((1)^2 +(3)^2) = sqrt(1+9) = sqrt(10) units`
` BE = sqrt((0-2)^2 +(1-1)^2) = sqrt((-2)^2 +(0)^2) = sqrt(4+0) = sqrt(4)= 2 units`
`CF = sqrt((1-0)^2 +(0-3)^2) = sqrt((1)^2 +(-3)^2) = sqrt(1+9) = sqrt(10) units`
`"Therefore, the lengths of the medians:" AD = sqrt(10) units . BE=2 units and CF = sqrt(10) units .`
APPEARS IN
संबंधित प्रश्न
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) such that AP =(2/5)AB.
Let P and Q be the points of trisection of the line segment joining the points A(2, -2) and B(-7, 4) such that P is nearer to A. Find the coordinates of P and Q.
Find the coordinates of the point which divides the join of (–1, 7) and (4, –3) in the ratio 2 : 3.
Find the ratio in which the line segment joining A (1, −5) and B (−4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
The line segment joining the points (3, -4) and (1, 2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and (5/3, q) respectively. Find the values of p and q.
A (2, 5), B (–1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that : AP : PB = AQ : QC = 1 : 2.
- Calculate the co-ordinates of P and Q.
- Show that : `PQ = 1/3 BC`.
- Write down the co-ordinates of the point P that divides the line joining A(−4, 1) and B(17, 10) in the ratio 1 : 2.
- Calculate the distance OP, where O is the origin.
- In what ratio does the y-axis divide the line AB?
If the point C (–1, 2) divides internally the line-segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x2 + y2 ?
The point Q divides segment joining A(3, 5) and B(7, 9) in the ratio 2 : 3. Find the X-coordinate of Q
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
