Advertisements
Advertisements
प्रश्न
Find the number of solid spheres, each of diameter 6 cm, that could be moulded to form a solid metallic cylinder of height 45 cm and diameter 4 cm.
उत्तर
We have,
Radius of the sphere, R `= 6/2 = 3 "cm" `
Radius of the cylinder, `"r" = 4/2 = 2 "cm"` and
Height of the cylinder, h = 45 cm
Now,
The number of solid spheres`= "Volume of the cylinder"/"Volume of the sphere"`
`=(pi"r"^2"h")/((4/3pi"R"^3))`
`=(3"r"^2"h")/(4"R"^3)`
`=(3xx2xx2xx45)/(4xx3xx3xx3)`
= 5
So, the number of solid spheres so moulded is 5.
APPEARS IN
संबंधित प्रश्न
Water flows at the rate of 15 km/hr through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide . In what time will the level of water in the pond rise by 21 cm.
The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheet required to make this bucket.
The radii of two cones are in the ratio 2 : 1 and their volumes are equal. What is the ratio of their heights?
A tent is in the shape of a right circular cylinder up to a height of 3 m and conical above it. The total height of the tent is 13.5 m and the radius of its base is 14 m. Find the cost of cloth required to make the tent at the rate of Rs 80 per square metre.
The volume of a cube is 729 cm3. Find its surface area.
66 cubic cm of silver is drawn into a wire 1 mm in diameter. Calculate the length of the wire in metres.
The curved surface area of a sphere is 5544 cm2. Find its volume.
A circus tent is cylindrical to a height of 4 m and conical above it. If its diameter is 105 m and its slant height is 40 m, the total area of canvas required is
Two identical cubes each of volume 64 cm3 are joined together end to end. What is the surface area of the resulting cuboid?
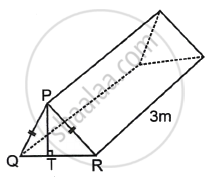
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent