Advertisements
Advertisements
प्रश्न
Find the relation connecting p and q, if the lines py = 2x + 5 and qx + 3y = 2 are parallel to each other.
उत्तर
Slope of py = 2x + 5 is `2/"p"`
Slope of line qx + 3y = 2 is `(-"q")/3`
Since the lines are given parallel their slopes must be equal
`therefore 2/"q" = (-"q")/3`
`therefore "pq" = -6`
APPEARS IN
संबंधित प्रश्न
Find the equation of the line passing through (5, –3) and parallel to x – 3y = 4.
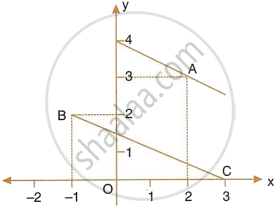
In the following diagram, write down:
- the co-ordinates of the points A, B and C.
- the equation of the line through A and parallel to BC.
Point P divides the line segment joining the points A(8, 0) and B(16, –8) in the ratio 3 : 5. Find its co-ordinates of point P. Also, find the equation of the line through P and parallel to 3x + 5y = 7.
Given a straight line x cos 30° + y sin 30° = 2. Determine the equation of the other line which is parallel to it and passes through (4, 3).
Find the value of k such that the line (k – 2)x + (k + 3)y – 5 = 0 is:
- perpendicular to the line 2x – y + 7 = 0
- parallel to it.
Find the slope of a line perpendicular to the foloowing line x - `(3"y")/2 + 1 = 0`
Find the slope of a line perpendicular to the foloowing line `(3"x")/4 -"y" = 5`
The lines px + 5y + 7 = 0 and 2y = 5x - 6 are perpendicular to ach other. Find p.
Find the relation connecting a and b, if the lines ay = 2x + 4 and 4y + bx = 2 are perpendicular to each other.
Find the equation of a line perpendicular to the join of A(3,5) and B(-1,7) if it passes through the midpoint of AB.
