Advertisements
Advertisements
प्रश्न
Find the resultant electric field due to an electric dipole of dipole moment, 2aq, (2a being the separation between the charges ±± q) at a point distant 'x' on its equator.
उत्तर
Consider a dipole consisting of two electric charges +q and −q between a small distance AB = 2a with centre O.
Now, let us find the electric field intensity at point P.
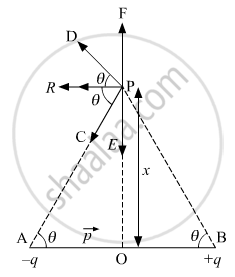
The magnitudes of the electric field at point P due to the two charges +q and −q are given by
`E_(+q) = q/(4πε_0) 1/(x^2+a^2) .....(1)`
and ` E_(-q) = q/(4πε_0) 1/(x^2+a^2) ...... (2)`
`∴ E_(+q) = E_(-q) `
The directions of E+q and E−q are as shown in the figure. The components normal to the dipole axis along PE and PF cancel away. The components along the dipole axis add up.
Therefore, the resultant electric field at point P is given as
`E = - (E_(+q) + E_(-q) cosΘ)` (The negative sign shows that the field is opposite to the dipole moment of the dipole.)
`E=(-2qa)/(4πε_0 (x^2+a^2)^(3/2)) ......(3)`
When point P lies at a large distance (x >> a) from the dipole, the above expression reduces to
`E = (-2qa)/(4πε_0 x^3 ) ....... (4)`
∴ `p =1 xx 2a`
∴ `E = (-p)/(4πε_0 x^3 )` (x >> a)
The direction of this electric field is along PR (or BA).
APPEARS IN
संबंधित प्रश्न
An electric dipole of dipole moment`vecp` consists of point charges +q and −q separated by a distance 2a apart. Deduce the expression for the electric field `vecE` due to the dipole at a distance x from the centre of the dipole on its axial line in terms of the dipole moment `vecp`. Hence show that in the limit x>> a, `vecE->2vecp"/"(4piepsilon_0x^3)`
Depict the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
An electric dipole of length 1 cm, which placed with its axis making an angle of 60° with uniform electric field, experience a torque of \[6\sqrt{3} Nm\] . Calculate the potential energy of the dipole if it has charge ±2 nC.
On the axis and on the equator of an electric dipole for all points ____________.
Electric charges q, q, - 2q are placed at the comers of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is ____________.
A conic surface is placed in a uniform electric field E as shown in the figure such that the field is perpendicular to the surface on the side AB. The base of the cone is of radius R, and the height of the cone is h. The angle of the cone is θ.
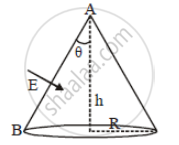
Find the magnitude of the flux that enters the cone's curved surface from the left side. Do not count the outgoing flux (θ < 45°)
The electric intensity due to a dipole of length 10 cm and having a charge of 500 µC, at a point on the axis at a distance 20 cm from one of the charges in air, is:
Polar molecules are the molecules ______.
The electric potential V as a function of distance X is shown in the figure.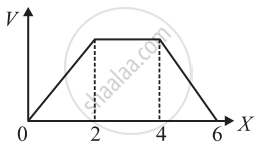
The graph of the magnitude of electric field intensity E as a function of X is ______.
In an electric dipole, what is the locus of a point having zero potential?
