Advertisements
Advertisements
प्रश्न
Find the resultant electric field due to an electric dipole of dipole moment, 2aq, (2a being the separation between the charges ±± q) at a point distant 'x' on its equator.
उत्तर
Consider a dipole consisting of two electric charges +q and −q between a small distance AB = 2a with centre O.
Now, let us find the electric field intensity at point P.
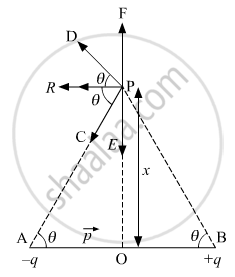
The magnitudes of the electric field at point P due to the two charges +q and −q are given by
`E_(+q) = q/(4πε_0) 1/(x^2+a^2) .....(1)`
and ` E_(-q) = q/(4πε_0) 1/(x^2+a^2) ...... (2)`
`∴ E_(+q) = E_(-q) `
The directions of E+q and E−q are as shown in the figure. The components normal to the dipole axis along PE and PF cancel away. The components along the dipole axis add up.
Therefore, the resultant electric field at point P is given as
`E = - (E_(+q) + E_(-q) cosΘ)` (The negative sign shows that the field is opposite to the dipole moment of the dipole.)
`E=(-2qa)/(4πε_0 (x^2+a^2)^(3/2)) ......(3)`
When point P lies at a large distance (x >> a) from the dipole, the above expression reduces to
`E = (-2qa)/(4πε_0 x^3 ) ....... (4)`
∴ `p =1 xx 2a`
∴ `E = (-p)/(4πε_0 x^3 )` (x >> a)
The direction of this electric field is along PR (or BA).
APPEARS IN
संबंधित प्रश्न
Drive the expression for electric field at a point on the equatorial line of an electric dipole.
Depict the equipotential surfaces due to an electric dipole.
It is said that the separation between the two charges forming an electric dipole should be small. In comparison to what should this separation be small?
An electric dipole is placed at the centre of a sphere. Mark the correct options.
(a) The flux of the electric field through the sphere is zero.
(b) The electric field is zero at every point of the sphere.
(c) The electric field is not zero anywhere on the sphere.
(d) The electric field is zero on a circle on the sphere.
A sample of HCI gas is placed in an electric field of 2.5 × 104 NC−1. The dipole moment of each HCI molecule is 3.4 × 10−30 Cm. Find the maximum torque that can act on a molecule.
Two-point charges Q1 = 400 μC and Q2 = 100 μC are kept fixed, 60 cm apart in a vacuum. Find the intensity of the electric field at the midpoint of the line joining Q1 and Q2.
Dimensions of mass in electric field and in electric dipole moment are respectively.
The electric intensity due to a dipole of length 10 cm and having a charge of 500 µC, at a point on the axis at a distance 20 cm from one of the charges in air, is:
What work must be done to rotate an electric dipole through an angle θ with the electric field, if an electric dipole of moment p is placed in a uniform electric field E with p parallel to E?
