Advertisements
Advertisements
प्रश्न
Find the slope of a line passing through the following point:
(−3, 2) and (1, 4)
उत्तर
(−3, 2) and (1, 4)
Let m be the slope of the given line.
\[\therefore m = \frac{y_2 - y_1}{x_2 - x_1}\]
\[ \Rightarrow m = \frac{4 - 2}{1 + 3} = \frac{2}{4} = \frac{1}{2}\]
Hence, the slope of the line passing through the points (−3, 2) and (1, 4) is \[\frac{1}{2}\].
APPEARS IN
संबंधित प्रश्न
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, –4) and B (8, 0).
Without using distance formula, show that points (–2, –1), (4, 0), (3, 3) and (–3, 2) are vertices of a parallelogram.
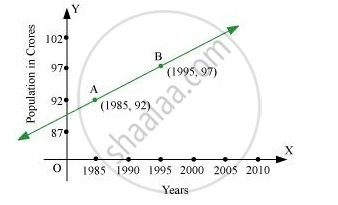
Consider the given population and year graph. Find the slope of the line AB and using it, find what will be the population in the year 2010?
Find the slope of the lines which make the following angle with the positive direction of x-axis: \[\frac{\pi}{3}\]
Find the slope of a line passing through the following point:
\[(a t_1^2 , 2 a t_1 ) \text { and } (a t_2^2 , 2 a t_2 )\]
State whether the two lines in each of the following is parallel, perpendicular or neither.
Through (6, 3) and (1, 1); through (−2, 5) and (2, −5)
What can be said regarding a line if its slope is positive ?
Show that the line joining (2, −3) and (−5, 1) is parallel to the line joining (7, −1) and (0, 3).
Prove that the points (−4, −1), (−2, −4), (4, 0) and (2, 3) are the vertices of a rectangle.
The slope of a line is double of the slope of another line. If tangents of the angle between them is \[\frac{1}{3}\],find the slopes of the other line.
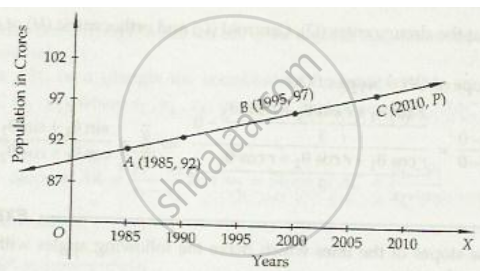
Consider the following population and year graph:
Find the slope of the line AB and using it, find what will be the population in the year 2010.
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear.
Find the equation of a straight line with slope −2 and intersecting the x-axis at a distance of 3 units to the left of origin.
Find the equation of a line which is perpendicular to the line joining (4, 2) and (3, 5) and cuts off an intercept of length 3 on y-axis.
Find the equation of the perpendicular to the line segment joining (4, 3) and (−1, 1) if it cuts off an intercept −3 from y-axis.
Find the equation of the strainght line intersecting y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Find the equations of the altitudes of a ∆ ABC whose vertices are A (1, 4), B (−3, 2) and C (−5, −3).
If the image of the point (2, 1) with respect to a line mirror is (5, 2), find the equation of the mirror.
Find the angles between the following pair of straight lines:
3x + y + 12 = 0 and x + 2y − 1 = 0
Prove that the straight lines (a + b) x + (a − b ) y = 2ab, (a − b) x + (a + b) y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is 2 tan−1 \[\left( \frac{a}{b} \right)\].
Write the coordinates of the image of the point (3, 8) in the line x + 3y − 7 = 0.
The equation of the line with slope −3/2 and which is concurrent with the lines 4x + 3y − 7 = 0 and 8x + 5y − 1 = 0 is
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y − 11 = 0 are
If x + y = k is normal to y2 = 12x, then k is ______.
If one diagonal of a square is along the line 8x – 15y = 0 and one of its vertex is at (1, 2), then find the equation of sides of the square passing through this vertex.
The intercept cut off by a line from y-axis is twice than that from x-axis, and the line passes through the point (1, 2). The equation of the line is ______.
The reflection of the point (4, – 13) about the line 5x + y + 6 = 0 is ______.
Find the equation of the line passing through the point (5, 2) and perpendicular to the line joining the points (2, 3) and (3, – 1).
Find the angle between the lines y = `(2 - sqrt(3)) (x + 5)` and y = `(2 + sqrt(3))(x - 7)`
Find the equation of one of the sides of an isosceles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2, 2).
P1, P2 are points on either of the two lines `- sqrt(3) |x|` = 2 at a distance of 5 units from their point of intersection. Find the coordinates of the foot of perpendiculars drawn from P1, P2 on the bisector of the angle between the given lines.
If p is the length of perpendicular from the origin on the line `x/a + y/b` = 1 and a2, p2, b2 are in A.P, then show that a4 + b4 = 0.
Equation of the line passing through (1, 2) and parallel to the line y = 3x – 1 is ______.
One vertex of the equilateral triangle with centroid at the origin and one side as x + y – 2 = 0 is ______.
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5, 3). The co-ordinates of the point A is ______.
The three straight lines ax + by = c, bx + cy = a and cx + ay = b are collinear, if ______.
If the line joining two points A (2, 0) and B (3, 1) is rotated about A in anticlockwise direction through an angle of 15°, then the equation of the line in new position is ______.
