Advertisements
Advertisements
प्रश्न
P1, P2 are points on either of the two lines `- sqrt(3) |x|` = 2 at a distance of 5 units from their point of intersection. Find the coordinates of the foot of perpendiculars drawn from P1, P2 on the bisector of the angle between the given lines.
Advertisements
उत्तर
Given lines are `- sqrt(3) |x|` = 2
⇒ `y - sqrt(3)x` = 2, if x ≥ 0 .....(i)
And `y + sqrt(3)x` = 2, if x < 0 ......(ii)
Slope of equation (i) is tan θ = `sqrt(3)`
∴ θ = 60°
Slope of equation (ii) is tan q `- sqrt(3)`
∴ θ = 120°
Solving equation (i) and equation (ii) we get
`y - sqrt(3) = 2`
`y + sqrt(3)x = 2`
2y = 4
⇒ y = 2
Putting the value of y is eq. (i) we get
x = 0
∴ Point of intersection of line (i) and (ii) is Q(0, 2)
∴ QO = 2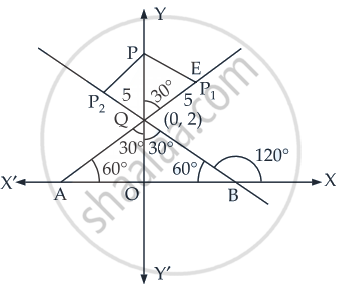
In ΔPEQ,
cos 30° = `"PQ"/"QE"`
`sqrt(3)/2 = "PQ"/5`
∴ PQ = `(5sqrt(3))/2`
∴ OP = OQ + PQ
= `2 + (5sqrt(3))/2`
Hence, the coordinates of the foot of perpendicular = `(0, 2 + (5sqrt(3))/02)`.
APPEARS IN
संबंधित प्रश्न
The base of an equilateral triangle with side 2a lies along they y-axis such that the mid point of the base is at the origin. Find vertices of the triangle.
Find the angle between the x-axis and the line joining the points (3, –1) and (4, –2).
The slope of a line is double of the slope of another line. If tangent of the angle between them is `1/3`, find the slopes of the lines.
Find the equation of a line drawn perpendicular to the line `x/4 + y/6 = 1`through the point, where it meets the y-axis.
Find the slope of the lines which make the following angle with the positive direction of x-axis:
\[\frac{2\pi}{3}\]
State whether the two lines in each of the following are parallel, perpendicular or neither.
Through (5, 6) and (2, 3); through (9, −2) and (6, −5)
State whether the two lines in each of the following is parallel, perpendicular or neither.
Through (3, 15) and (16, 6); through (−5, 3) and (8, 2).
Find the slope of a line (i) which bisects the first quadrant angle (ii) which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Using the method of slope, show that the following points are collinear A (16, − 18), B (3, −6), C (−10, 6) .
What can be said regarding a line if its slope is zero ?
What can be said regarding a line if its slope is negative?
The slope of a line is double of the slope of another line. If tangents of the angle between them is \[\frac{1}{3}\],find the slopes of the other line.
Without using the distance formula, show that points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
Find the angle between the X-axis and the line joining the points (3, −1) and (4, −2).
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Find the angles between the following pair of straight lines:
3x − y + 5 = 0 and x − 3y + 1 = 0
Find the acute angle between the lines 2x − y + 3 = 0 and x + y + 2 = 0.
Prove that the points (2, −1), (0, 2), (2, 3) and (4, 0) are the coordinates of the vertices of a parallelogram and find the angle between its diagonals.
Find the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1.
Prove that the straight lines (a + b) x + (a − b ) y = 2ab, (a − b) x + (a + b) y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is 2 tan−1 \[\left( \frac{a}{b} \right)\].
Show that the line a2x + ay + 1 = 0 is perpendicular to the line x − ay = 1 for all non-zero real values of a.
The angle between the lines 2x − y + 3 = 0 and x + 2y + 3 = 0 is
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y − 11 = 0 are
If m1 and m2 are slopes of lines represented by 6x2 - 5xy + y2 = 0, then (m1)3 + (m2)3 = ?
The line passing through (– 2, 0) and (1, 3) makes an angle of ______ with X-axis.
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5, 3). Find the coordinates of the point A.
The two lines ax + by = c and a′x + b′y = c′ are perpendicular if ______.
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y – 11 = 0 are ______.
The intercept cut off by a line from y-axis is twice than that from x-axis, and the line passes through the point (1, 2). The equation of the line is ______.
Find the equation of a straight line on which length of perpendicular from the origin is four units and the line makes an angle of 120° with the positive direction of x-axis.
The tangent of angle between the lines whose intercepts on the axes are a, – b and b, – a, respectively, is ______.
Equation of the line passing through (1, 2) and parallel to the line y = 3x – 1 is ______.
The point (4, 1) undergoes the following two successive transformations:
(i) Reflection about the line y = x
(ii) Translation through a distance 2 units along the positive x-axis Then the final coordinates of the point are ______.
The vertex of an equilateral triangle is (2, 3) and the equation of the opposite side is x + y = 2. Then the other two sides are y – 3 = `(2 +- sqrt(3)) (x - 2)`.
The equation of the line through the intersection of the lines 2x – 3y = 0 and 4x – 5y = 2 and
| Column C1 | Column C2 |
| (a) Through the point (2, 1) is | (i) 2x – y = 4 |
| (b) Perpendicular to the line (ii) x + y – 5 = 0 x + 2y + 1 = 0 is |
(ii) x + y – 5 = 0 |
| (c) Parallel to the line (iii) x – y –1 = 0 3x – 4y + 5 = 0 is |
(iii) x – y –1 = 0 |
| (d) Equally inclined to the axes is | (iv) 3x – 4y – 1 = 0 |
If the line joining two points A (2, 0) and B (3, 1) is rotated about A in anticlockwise direction through an angle of 15°, then the equation of the line in new position is ______.
