Advertisements
Advertisements
प्रश्न
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5, 3). Find the coordinates of the point A.
उत्तर
Let the incident ray strike x-axis at the point A whose coordinates be (x, 0).
From the figure, the slope of the reflected ray is given by
tan θ = `3/(5 - x)` .....(1)
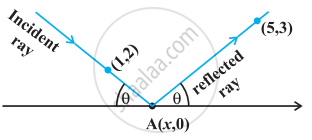
Again, the slope of the incident ray is given by
`tan(pi - theta) = (-2)/(x - 1)` (Why?)
or `- tan theta = (-2)/(x - 1)` ....(2)
Solving (1) and (2), we get
`3/(5 - x) = 2/(x - 1)` or x = `13/5`
Therefore, the required coordinates of the point A are `13/5, 0`.
APPEARS IN
संबंधित प्रश्न
Draw a quadrilateral in the Cartesian plane, whose vertices are (–4, 5), (0, 7), (5, –5) and (–4, –2). Also, find its area.
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
The slope of a line is double of the slope of another line. If tangent of the angle between them is `1/3`, find the slopes of the lines.
If three point (h, 0), (a, b) and (0, k) lie on a line, show that `q/h + b/k = 1`
Find the equation of a line drawn perpendicular to the line `x/4 + y/6 = 1`through the point, where it meets the y-axis.
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
Find the slope of the lines which make the following angle with the positive direction of x-axis:
\[\frac{2\pi}{3}\]
Find the slope of a line (i) which bisects the first quadrant angle (ii) which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Without using Pythagoras theorem, show that the points A (0, 4), B (1, 2) and C (3, 3) are the vertices of a right angled triangle.
Prove that the points (−4, −1), (−2, −4), (4, 0) and (2, 3) are the vertices of a rectangle.
If three points A (h, 0), P (a, b) and B (0, k) lie on a line, show that: \[\frac{a}{h} + \frac{b}{k} = 1\].
The slope of a line is double of the slope of another line. If tangents of the angle between them is \[\frac{1}{3}\],find the slopes of the other line.
By using the concept of slope, show that the points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
Find the equation of a straight line with slope −2 and intersecting the x-axis at a distance of 3 units to the left of origin.
Find the tangent of the angle between the lines which have intercepts 3, 4 and 1, 8 on the axes respectively.
If the slopes of the lines given by the equation ax2 + 2hxy + by2 = 0 are in the ratio 5 : 3, then the ratio h2 : ab = ______.
The equation of a line passing through the point (7, - 4) and perpendicular to the line passing through the points (2, 3) and (1 , - 2 ) is ______.
The line passing through (– 2, 0) and (1, 3) makes an angle of ______ with X-axis.
If the slope of a line passing through the point A(3, 2) is `3/4`, then find points on the line which are 5 units away from the point A.
Find the equation to the straight line passing through the point of intersection of the lines 5x – 6y – 1 = 0 and 3x + 2y + 5 = 0 and perpendicular to the line 3x – 5y + 11 = 0.
Show that the tangent of an angle between the lines `x/a + y/b` = 1 and `x/a - y/b` = 1 is `(2ab)/(a^2 - b^2)`
The equation of the straight line passing through the point (3, 2) and perpendicular to the line y = x is ______.
One vertex of the equilateral triangle with centroid at the origin and one side as x + y – 2 = 0 is ______.
Equations of the lines through the point (3, 2) and making an angle of 45° with the line x – 2y = 3 are ______.
The equation of the line through the intersection of the lines 2x – 3y = 0 and 4x – 5y = 2 and
| Column C1 | Column C2 |
| (a) Through the point (2, 1) is | (i) 2x – y = 4 |
| (b) Perpendicular to the line (ii) x + y – 5 = 0 x + 2y + 1 = 0 is |
(ii) x + y – 5 = 0 |
| (c) Parallel to the line (iii) x – y –1 = 0 3x – 4y + 5 = 0 is |
(iii) x – y –1 = 0 |
| (d) Equally inclined to the axes is | (iv) 3x – 4y – 1 = 0 |
If the line joining two points A (2, 0) and B (3, 1) is rotated about A in anticlockwise direction through an angle of 15°, then the equation of the line in new position is ______.
