Advertisements
Advertisements
प्रश्न
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
उत्तर
If points A (x, –1), B (2, 1), and C (4, 5) are collinear, then
Slope of AB = Slope of BC

APPEARS IN
संबंधित प्रश्न
The base of an equilateral triangle with side 2a lies along they y-axis such that the mid point of the base is at the origin. Find vertices of the triangle.
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Without using distance formula, show that points (–2, –1), (4, 0), (3, 3) and (–3, 2) are vertices of a parallelogram.
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x –2y = 3.
State whether the two lines in each of the following is parallel, perpendicular or neither.
Through (6, 3) and (1, 1); through (−2, 5) and (2, −5)
What can be said regarding a line if its slope is zero ?
What can be said regarding a line if its slope is positive ?
The slope of a line is double of the slope of another line. If tangents of the angle between them is \[\frac{1}{3}\],find the slopes of the other line.
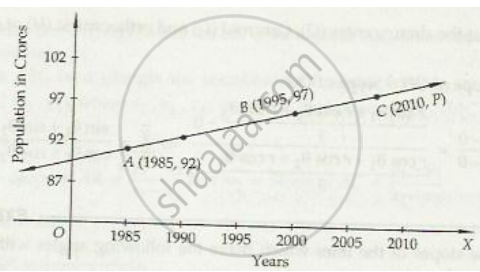
Consider the following population and year graph:
Find the slope of the line AB and using it, find what will be the population in the year 2010.
Find the equation of a straight line with slope 2 and y-intercept 3 .
Find the equation of a straight line with slope −2 and intersecting the x-axis at a distance of 3 units to the left of origin.
Find the equation of the strainght line intersecting y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Show that the perpendicular bisectors of the sides of a triangle are concurrent.
Find the equations of the altitudes of a ∆ ABC whose vertices are A (1, 4), B (−3, 2) and C (−5, −3).
Find the angles between the following pair of straight lines:
3x + 4y − 7 = 0 and 4x − 3y + 5 = 0
Find the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1.
Show that the line a2x + ay + 1 = 0 is perpendicular to the line x − ay = 1 for all non-zero real values of a.
The angle between the lines 2x − y + 3 = 0 and x + 2y + 3 = 0 is
The medians AD and BE of a triangle with vertices A (0, b), B (0, 0) and C (a, 0) are perpendicular to each other, if
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y − 11 = 0 are
Find k, if the slope of one of the lines given by kx2 + 8xy + y2 = 0 exceeds the slope of the other by 6.
If m1 and m2 are slopes of lines represented by 6x2 - 5xy + y2 = 0, then (m1)3 + (m2)3 = ?
The equation of a line passing through the point (7, - 4) and perpendicular to the line passing through the points (2, 3) and (1 , - 2 ) is ______.
Point of the curve y2 = 3(x – 2) at which the normal is parallel to the line 2y + 4x + 5 = 0 is ______.
If the line joining two points A(2, 0) and B(3, 1) is rotated about A in anticlock wise direction through an angle of 15°. Find the equation of the line in new position.
If the slope of a line passing through the point A(3, 2) is `3/4`, then find points on the line which are 5 units away from the point A.
If one diagonal of a square is along the line 8x – 15y = 0 and one of its vertex is at (1, 2), then find the equation of sides of the square passing through this vertex.
The intercept cut off by a line from y-axis is twice than that from x-axis, and the line passes through the point (1, 2). The equation of the line is ______.
Find the equation of the line passing through the point (5, 2) and perpendicular to the line joining the points (2, 3) and (3, – 1).
Find the equation of one of the sides of an isosceles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2, 2).
Equation of the line passing through (1, 2) and parallel to the line y = 3x – 1 is ______.
If the vertices of a triangle have integral coordinates, then the triangle can not be equilateral.
The points A(– 2, 1), B(0, 5), C(– 1, 2) are collinear.
Line joining the points (3, – 4) and (– 2, 6) is perpendicular to the line joining the points (–3, 6) and (9, –18).
The line which passes through the origin and intersect the two lines `(x - 1)/2 = (y + 3)/4 = (z - 5)/3, (x - 4)/2 = (y + 3)/3 = (z - 14)/4`, is ______.
