Advertisements
Advertisements
प्रश्न
Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
उत्तर
If a line makes an angle of 30° with the positive direction of the y-axis measured anticlockwise, then the angle made by the line with the positive direction of the x-axis measured anticlockwise is 90° + 30° = 120°.
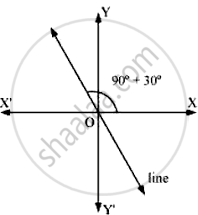
Thus, the slope of the given line is tan 120° = tan (180° – 60°) = –tan 60° = `-sqrt3`
APPEARS IN
संबंधित प्रश्न
Draw a quadrilateral in the Cartesian plane, whose vertices are (–4, 5), (0, 7), (5, –5) and (–4, –2). Also, find its area.
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, –4) and B (8, 0).
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
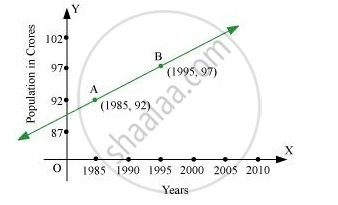
Consider the given population and year graph. Find the slope of the line AB and using it, find what will be the population in the year 2010?
Find the values of k for which the line (k–3) x – (4 – k2) y + k2 –7k + 6 = 0 is
- Parallel to the x-axis,
- Parallel to the y-axis,
- Passing through the origin.
Find the equation of a line drawn perpendicular to the line `x/4 + y/6 = 1`through the point, where it meets the y-axis.
Find the slope of the lines which make the following angle with the positive direction of x-axis:
\[\frac{3\pi}{4}\]
Find the slope of a line passing through the following point:
(−3, 2) and (1, 4)
Find the slope of a line passing through the following point:
\[(a t_1^2 , 2 a t_1 ) \text { and } (a t_2^2 , 2 a t_2 )\]
State whether the two lines in each of the following are parallel, perpendicular or neither.
Through (5, 6) and (2, 3); through (9, −2) and (6, −5)
Find the slope of a line (i) which bisects the first quadrant angle (ii) which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
What can be said regarding a line if its slope is positive ?
If three points A (h, 0), P (a, b) and B (0, k) lie on a line, show that: \[\frac{a}{h} + \frac{b}{k} = 1\].
A quadrilateral has vertices (4, 1), (1, 7), (−6, 0) and (−1, −9). Show that the mid-points of the sides of this quadrilateral form a parallelogram.
Find the equation of a straight line with slope − 1/3 and y-intercept − 4.
Find the equations of the bisectors of the angles between the coordinate axes.
Find the equations of the altitudes of a ∆ ABC whose vertices are A (1, 4), B (−3, 2) and C (−5, −3).
Find the equation of the right bisector of the line segment joining the points (3, 4) and (−1, 2).
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Find the angles between the following pair of straight lines:
3x + y + 12 = 0 and x + 2y − 1 = 0
Find the angles between the following pair of straight lines:
3x − y + 5 = 0 and x − 3y + 1 = 0
Find the angles between the following pair of straight lines:
x − 4y = 3 and 6x − y = 11
Find the acute angle between the lines 2x − y + 3 = 0 and x + y + 2 = 0.
Find the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1.
Prove that the straight lines (a + b) x + (a − b ) y = 2ab, (a − b) x + (a + b) y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is 2 tan−1 \[\left( \frac{a}{b} \right)\].
The angle between the lines 2x − y + 3 = 0 and x + 2y + 3 = 0 is
If x + y = k is normal to y2 = 12x, then k is ______.
Point of the curve y2 = 3(x – 2) at which the normal is parallel to the line 2y + 4x + 5 = 0 is ______.
The two lines ax + by = c and a′x + b′y = c′ are perpendicular if ______.
Show that the tangent of an angle between the lines `x/a + y/b` = 1 and `x/a - y/b` = 1 is `(2ab)/(a^2 - b^2)`
A variable line passes through a fixed point P. The algebraic sum of the perpendiculars drawn from the points (2, 0), (0, 2) and (1, 1) on the line is zero. Find the coordinates of the point P.
The tangent of angle between the lines whose intercepts on the axes are a, – b and b, – a, respectively, is ______.
The coordinates of the foot of perpendiculars from the point (2, 3) on the line y = 3x + 4 is given by ______.
The points (3, 4) and (2, – 6) are situated on the ______ of the line 3x – 4y – 8 = 0.
If the vertices of a triangle have integral coordinates, then the triangle can not be equilateral.
Line joining the points (3, – 4) and (– 2, 6) is perpendicular to the line joining the points (–3, 6) and (9, –18).
