Advertisements
Advertisements
प्रश्न
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
उत्तर
If points A (x, –1), B (2, 1), and C (4, 5) are collinear, then
Slope of AB = Slope of BC

APPEARS IN
संबंधित प्रश्न
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
Without using distance formula, show that points (–2, –1), (4, 0), (3, 3) and (–3, 2) are vertices of a parallelogram.
The slope of a line is double of the slope of another line. If tangent of the angle between them is `1/3`, find the slopes of the lines.
A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m (h – x1).
Find the values of k for which the line (k–3) x – (4 – k2) y + k2 –7k + 6 = 0 is
- Parallel to the x-axis,
- Parallel to the y-axis,
- Passing through the origin.
Find the equation of a line drawn perpendicular to the line `x/4 + y/6 = 1`through the point, where it meets the y-axis.
Find the slope of the lines which make the following angle with the positive direction of x-axis:
\[- \frac{\pi}{4}\]
Find the slope of the lines which make the following angle with the positive direction of x-axis: \[\frac{\pi}{3}\]
Find the slope of a line passing through the following point:
\[(a t_1^2 , 2 a t_1 ) \text { and } (a t_2^2 , 2 a t_2 )\]
State whether the two lines in each of the following is parallel, perpendicular or neither.
Through (3, 15) and (16, 6); through (−5, 3) and (8, 2).
Find the slope of a line (i) which bisects the first quadrant angle (ii) which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
What is the value of y so that the line through (3, y) and (2, 7) is parallel to the line through (−1, 4) and (0, 6)?
What can be said regarding a line if its slope is negative?
Show that the line joining (2, −5) and (−2, 5) is perpendicular to the line joining (6, 3) and (1, 1).
Prove that the points (−4, −1), (−2, −4), (4, 0) and (2, 3) are the vertices of a rectangle.
The slope of a line is double of the slope of another line. If tangents of the angle between them is \[\frac{1}{3}\],find the slopes of the other line.
Consider the following population and year graph:
Find the slope of the line AB and using it, find what will be the population in the year 2010.
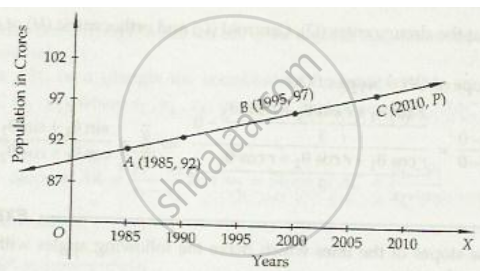
Find the angle between the X-axis and the line joining the points (3, −1) and (4, −2).
Find the angle between X-axis and the line joining the points (3, −1) and (4, −2).
A quadrilateral has vertices (4, 1), (1, 7), (−6, 0) and (−1, −9). Show that the mid-points of the sides of this quadrilateral form a parallelogram.
Show that the perpendicular bisectors of the sides of a triangle are concurrent.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (−1, 2).
Find the angles between the following pair of straight lines:
(m2 − mn) y = (mn + n2) x + n3 and (mn + m2) y = (mn − n2) x + m3.
If θ is the angle which the straight line joining the points (x1, y1) and (x2, y2) subtends at the origin, prove that \[\tan \theta = \frac{x_2 y_1 - x_1 y_2}{x_1 x_2 + y_1 y_2}\text { and } \cos \theta = \frac{x_1 x_2 + y_1 y_2}{\sqrt{{x_1}^2 + {y_1}^2}\sqrt{{x_2}^2 + {y_2}^2}}\].
Find the tangent of the angle between the lines which have intercepts 3, 4 and 1, 8 on the axes respectively.
The angle between the lines 2x − y + 3 = 0 and x + 2y + 3 = 0 is
The medians AD and BE of a triangle with vertices A (0, b), B (0, 0) and C (a, 0) are perpendicular to each other, if
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y − 11 = 0 are
The equation of a line passing through the point (7, - 4) and perpendicular to the line passing through the points (2, 3) and (1 , - 2 ) is ______.
If x + y = k is normal to y2 = 12x, then k is ______.
The two lines ax + by = c and a′x + b′y = c′ are perpendicular if ______.
Find the angle between the lines y = `(2 - sqrt(3)) (x + 5)` and y = `(2 + sqrt(3))(x - 7)`
Find the equation of one of the sides of an isosceles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2, 2).
If the equation of the base of an equilateral triangle is x + y = 2 and the vertex is (2, – 1), then find the length of the side of the triangle.
Equation of the line passing through (1, 2) and parallel to the line y = 3x – 1 is ______.
The point (4, 1) undergoes the following two successive transformations:
(i) Reflection about the line y = x
(ii) Translation through a distance 2 units along the positive x-axis Then the final coordinates of the point are ______.
