Advertisements
Advertisements
प्रश्न
A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m (h – x1).
उत्तर
The slope of the line passing through (x, y) and (h, k) is `(k - y_1)/(h - x_1)`
It is given that the slope of the line is m.
`("k" - "y"_1)/("h" - "x"_1) = "m"`
= k – y1 = m(h – x1)
Hence, k – y1 = m(h – x1)
APPEARS IN
संबंधित प्रश्न
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
Find the angle between the x-axis and the line joining the points (3, –1) and (4, –2).
If three point (h, 0), (a, b) and (0, k) lie on a line, show that `q/h + b/k = 1`
Find the equation of a line drawn perpendicular to the line `x/4 + y/6 = 1`through the point, where it meets the y-axis.
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
Find the slope of the lines which make the following angle with the positive direction of x-axis:
\[- \frac{\pi}{4}\]
Using the method of slope, show that the following points are collinear A (16, − 18), B (3, −6), C (−10, 6) .
What can be said regarding a line if its slope is positive ?
Show that the line joining (2, −3) and (−5, 1) is parallel to the line joining (7, −1) and (0, 3).
Without using Pythagoras theorem, show that the points A (0, 4), B (1, 2) and C (3, 3) are the vertices of a right angled triangle.
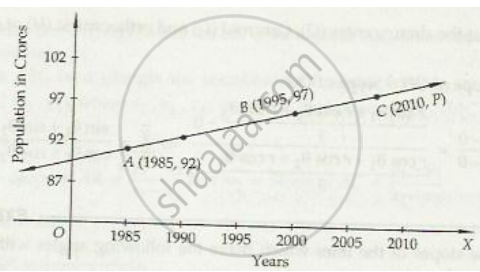
Consider the following population and year graph:
Find the slope of the line AB and using it, find what will be the population in the year 2010.
By using the concept of slope, show that the points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
Find the equations of the bisectors of the angles between the coordinate axes.
Find the equation of the perpendicular to the line segment joining (4, 3) and (−1, 1) if it cuts off an intercept −3 from y-axis.
Find the equations of the altitudes of a ∆ ABC whose vertices are A (1, 4), B (−3, 2) and C (−5, −3).
If the image of the point (2, 1) with respect to a line mirror is (5, 2), find the equation of the mirror.
The line through (h, 3) and (4, 1) intersects the line 7x − 9y − 19 = 0 at right angle. Find the value of h.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Find the angles between the following pair of straight lines:
3x + y + 12 = 0 and x + 2y − 1 = 0
Find the angles between the following pair of straight lines:
3x − y + 5 = 0 and x − 3y + 1 = 0
Find the angles between the following pair of straight lines:
x − 4y = 3 and 6x − y = 11
Find the angles between the following pair of straight lines:
(m2 − mn) y = (mn + n2) x + n3 and (mn + m2) y = (mn − n2) x + m3.
Prove that the straight lines (a + b) x + (a − b ) y = 2ab, (a − b) x + (a + b) y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is 2 tan−1 \[\left( \frac{a}{b} \right)\].
Show that the tangent of an angle between the lines \[\frac{x}{a} + \frac{y}{b} = 1 \text { and } \frac{x}{a} - \frac{y}{b} = 1\text { is } \frac{2ab}{a^2 - b^2}\].
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y − 11 = 0 are
The equation of a line passing through the point (7, - 4) and perpendicular to the line passing through the points (2, 3) and (1 , - 2 ) is ______.
Point of the curve y2 = 3(x – 2) at which the normal is parallel to the line 2y + 4x + 5 = 0 is ______.
If the slope of a line passing through the point A(3, 2) is `3/4`, then find points on the line which are 5 units away from the point A.
Find the equation to the straight line passing through the point of intersection of the lines 5x – 6y – 1 = 0 and 3x + 2y + 5 = 0 and perpendicular to the line 3x – 5y + 11 = 0.
The two lines ax + by = c and a′x + b′y = c′ are perpendicular if ______.
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y – 11 = 0 are ______.
The intercept cut off by a line from y-axis is twice than that from x-axis, and the line passes through the point (1, 2). The equation of the line is ______.
Slope of a line which cuts off intercepts of equal lengths on the axes is ______.
The equation of the straight line passing through the point (3, 2) and perpendicular to the line y = x is ______.
The coordinates of the foot of perpendiculars from the point (2, 3) on the line y = 3x + 4 is given by ______.
The points A(– 2, 1), B(0, 5), C(– 1, 2) are collinear.
The line which passes through the origin and intersect the two lines `(x - 1)/2 = (y + 3)/4 = (z - 5)/3, (x - 4)/2 = (y + 3)/3 = (z - 14)/4`, is ______.
