Advertisements
Advertisements
प्रश्न
The coordinates of the foot of perpendiculars from the point (2, 3) on the line y = 3x + 4 is given by ______.
पर्याय
`37/10, (-1)/10`
`(-1)/10, 37/10`
`10/37, -10`
`2/3, -1/3`
Advertisements
उत्तर
The coordinates of the foot of perpendiculars from the point (2, 3) on the line y = 3x + 4 is given by `(-1)/10, 37/10`.
Explanation:
Given equation is y = 3x + 4 .....(i)
⇒ 3x – y + 4 = 0
Slope = 3
Equation of any line passing through the point (2, 3) is
y – 3 = m(x – 2) .....(ii)
If equation (i) is perpendicular to eq. (ii)
Then m × 3 = – 1 ......`[because m_1 xx m_2 = - 1]`
⇒ m = `- 1/3`
Putting the value of m in equation (ii) we get
y – 3 = `- 1/3(x - 2)`
⇒ 3y – 9 = – x + 2
⇒ x + 3y = 11 .....(iii)
Solving equation (i) and equation (iii) we get
3x – y = – 4
⇒ y = 3x + 4 ......(iv)
Putting the value of y in eq. (iii) we get
x + 3(3x + 4) = 11
⇒ x + 9x + 12 = 11
⇒ 10x = – 1
⇒ x = `(-1)/10`
From equation (iv) we get
y = `3((-1)/10) + 4`
⇒ y = `(-3)/10 + 4`
⇒ y = `37/10`
So the required coordinates are `((-1)/10, 37/10)`.
APPEARS IN
संबंधित प्रश्न
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, –4) and B (8, 0).
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m (h – x1).
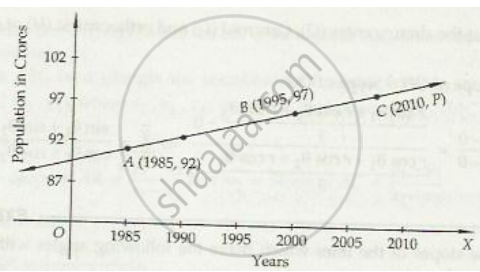
Consider the given population and year graph. Find the slope of the line AB and using it, find what will be the population in the year 2010?
Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x –2y = 3.
Find the slope of the lines which make the following angle with the positive direction of x-axis: \[\frac{\pi}{3}\]
State whether the two lines in each of the following are parallel, perpendicular or neither.
Through (9, 5) and (−1, 1); through (3, −5) and (8, −3)
State whether the two lines in each of the following is parallel, perpendicular or neither.
Through (3, 15) and (16, 6); through (−5, 3) and (8, 2).
Using the method of slope, show that the following points are collinear A (16, − 18), B (3, −6), C (−10, 6) .
Show that the line joining (2, −5) and (−2, 5) is perpendicular to the line joining (6, 3) and (1, 1).
Without using the distance formula, show that points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear.
By using the concept of slope, show that the points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
A quadrilateral has vertices (4, 1), (1, 7), (−6, 0) and (−1, −9). Show that the mid-points of the sides of this quadrilateral form a parallelogram.
Find the equation of a straight line with slope 2 and y-intercept 3 .
Find the equation of a line which is perpendicular to the line joining (4, 2) and (3, 5) and cuts off an intercept of length 3 on y-axis.
Find the equation of the perpendicular to the line segment joining (4, 3) and (−1, 1) if it cuts off an intercept −3 from y-axis.
Find the equations of the altitudes of a ∆ ABC whose vertices are A (1, 4), B (−3, 2) and C (−5, −3).
Find the angles between the following pair of straight lines:
3x + y + 12 = 0 and x + 2y − 1 = 0
Find the acute angle between the lines 2x − y + 3 = 0 and x + y + 2 = 0.
Find the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1.
Show that the line a2x + ay + 1 = 0 is perpendicular to the line x − ay = 1 for all non-zero real values of a.
The equation of the line with slope −3/2 and which is concurrent with the lines 4x + 3y − 7 = 0 and 8x + 5y − 1 = 0 is
The reflection of the point (4, −13) about the line 5x + y + 6 = 0 is
If m1 and m2 are slopes of lines represented by 6x2 - 5xy + y2 = 0, then (m1)3 + (m2)3 = ?
Find the equation to the straight line passing through the point of intersection of the lines 5x – 6y – 1 = 0 and 3x + 2y + 5 = 0 and perpendicular to the line 3x – 5y + 11 = 0.
Find the equation of one of the sides of an isosceles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2, 2).
P1, P2 are points on either of the two lines `- sqrt(3) |x|` = 2 at a distance of 5 units from their point of intersection. Find the coordinates of the foot of perpendiculars drawn from P1, P2 on the bisector of the angle between the given lines.
Slope of a line which cuts off intercepts of equal lengths on the axes is ______.
The point (4, 1) undergoes the following two successive transformations:
(i) Reflection about the line y = x
(ii) Translation through a distance 2 units along the positive x-axis Then the final coordinates of the point are ______.
One vertex of the equilateral triangle with centroid at the origin and one side as x + y – 2 = 0 is ______.
If the vertices of a triangle have integral coordinates, then the triangle can not be equilateral.
Line joining the points (3, – 4) and (– 2, 6) is perpendicular to the line joining the points (–3, 6) and (9, –18).
The three straight lines ax + by = c, bx + cy = a and cx + ay = b are collinear, if ______.
The lines whose vector equations are `r = 2hati - 3hatj + 7hatk + lambda (2hati + phatj + 5hatk) and r = hati - 2hatj + 3hatk + µ(3hati + phatj + phatk)` are perpendicular for all values of λ and µ if p =
