Advertisements
Advertisements
प्रश्न
If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2), then the equation of the line will be ______.
पर्याय
2x + 3y = 12
3x + 2y = 12
4x – 3y = 6
5x – 2y = 10
उत्तर
If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2), then the equation of the line will be 2x + 3y = 12.
Explanation:
Let the given line meets the axes at A(a, 0) and B(0, b).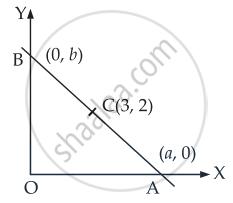
Given that C(3, 2) is the mid-point of AB
∴ 3 = (a + 0)/2`
⇒ a = 6
And 2 = `(0 + b)/2`
⇒ b = 4
Intercept form of the line AB
`x/a + y/b` = 1
⇒ `x/6 + y/4` = 1
⇒ 2x + 3y = 12
APPEARS IN
संबंधित प्रश्न
Find equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (–2, 3).
Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is A (x –x1) + B (y – y1) = 0.
If p and q are the lengths of perpendiculars from the origin to the lines x cos θ – y sin θ = k cos 2θ and xsec θ+ y cosec θ = k, respectively, prove that p2 + 4q2 = k2.
Find the equation of a line which is equidistant from the lines x = − 2 and x = 6.
Find the equation of a line that has y-intercept −4 and is parallel to the line joining (2, −5) and (1, 2).
Find the lines through the point (0, 2) making angles \[\frac{\pi}{3} \text { and } \frac{2\pi}{3}\] with the x-axis. Also, find the lines parallel to them cutting the y-axis at a distance of 2 units below the origin.
Find the equation of the side BC of the triangle ABC whose vertices are (−1, −2), (0, 1) and (2, 0) respectively. Also, find the equation of the median through (−1, −2).
Find the equation of a line for p = 4, α = 150°.
Find the equation of the line on which the length of the perpendicular segment from the origin to the line is 4 and the inclination of the perpendicular segment with the positive direction of x-axis is 30°.
Find the equation of the straight line on which the length of the perpendicular from the origin is 2 and the perpendicular makes an angle α with x-axis such that sin α = \[\frac{1}{3}\].
The length of the perpendicular from the origin to a line is 7 and the line makes an angle of 150° with the positive direction of Y-axis. Find the equation of the line.
Find the values of θ and p, if the equation x cos θ + y sin θ = p is the normal form of the line \[\sqrt{3}x + y + 2 = 0\].
Find the coordinates of the vertices of a triangle, the equations of whose sides are
y (t1 + t2) = 2x + 2a t1t2, y (t2 + t3) = 2x + 2a t2t3 and, y (t3 + t1) = 2x + 2a t1t3.
Find the area of the triangle formed by the line x + y − 6 = 0, x − 3y − 2 = 0 and 5x − 3y + 2 = 0.
Find the conditions that the straight lines y = m1 x + c1, y = m2 x + c2 and y = m3 x + c3 may meet in a point.
If the three lines ax + a2y + 1 = 0, bx + b2y + 1 = 0 and cx + c2y + 1 = 0 are concurrent, show that at least two of three constants a, b, c are equal.
Find the equation of the perpendicular bisector of the line joining the points (1, 3) and (3, 1).
Find the equation of the straight line perpendicular to 2x − 3y = 5 and cutting off an intercept 1 on the positive direction of the x-axis.
Find the values of α so that the point P (α2, α) lies inside or on the triangle formed by the lines x − 5y+ 6 = 0, x − 3y + 2 = 0 and x − 2y − 3 = 0.
The figure formed by the lines ax ± by ± c = 0 is
Two vertices of a triangle are (−2, −1) and (3, 2) and third vertex lies on the line x + y = 5. If the area of the triangle is 4 square units, then the third vertex is
Reduce the following equation into slope-intercept form and find their slopes and the y-intercepts.
x + 7y = 0
Reduce the following equation into slope-intercept form and find their slopes and the y-intercepts.
6x + 3y – 5 = 0
