Advertisements
Advertisements
प्रश्न
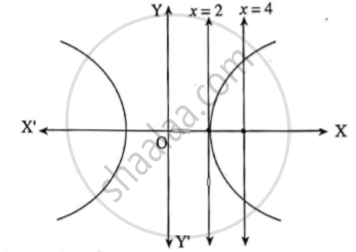
Find the volume of the solid obtained by revolving about the X-axis, the region bounded by the curve `"x"^2/4 - "y"^2/9 = 1` and the lines x = 2 , x = 4.
उत्तर
Given equation of the curve is
`"x"^2/4 - "y"^2/9 = 1` , which is a hyperbola
`therefore "y"^2/9 = "x"^2/4 - 1`
`therefore "y"^2 = 9/4 ("x"^2 - 4)`
`therefore "Volume" = pi int_2^4 "y"^2 "dx"`
`= (9pi)/4 int _2^4 ("x"^2 - 4) "dx"`
`therefore "V" = (9pi)/4 ["x"^3/3 - 4"x"]_2^4`
`= (9pi)/4 [(64/3 - 16) - (8/3 - 8)]`
= 24 π cubic units.
APPEARS IN
संबंधित प्रश्न
Evaluate : `int (1+logx)/(x(2+logx)(3+logx))dx`
Evaluate : `∫_0^(pi/2) (sinx.cosx)/(1 + sin^4x)`.dx
Integrate the following functions with respect to x :
`(1 + cos 4x)/(cos x - tan x)`
Integrate the following with respect to x :
`x^2/(1 + x^6)`
Integrate the following with respect to x :
`("e"^x - "e"^-x)/("e"^x + "e"^-x)`
Integrate the following with respect to x :
`("cosec" x)/(log(tan x/2))`
Integrate the following with respect to x :
`(sin 2x)/("a"^2 + "b"^2 sin^2x)`
Integrate the following with respect to x :
x(1 – x)17
Integrate the following with respect to x:
x2 cos x
Integrate the following with respect to x:
x5ex2
Integrate the following with respect to x:
`sin^-1 ((2x)/(1 + x^2))`
Find the integrals of the following:
`1/sqrt(xx^2 + 4x + 2)`
Find the integrals of the following:
`1/sqrt(9 + 8x - x^2)`
Integrate the following with respect to x:
`(5x - 2)/(2 + 2x + x^2)`
Integrate the following with respect to x:
`(x + 2)/sqrt(x^2 - 1)`
Integrate the following functions with respect to x:
`sqrt(81 + (2x + 1)^2`
Choose the correct alternative:
`int ("e"^(6 log x) - "e"^(5logx))/("e"^(4logx) - "e"^(3logx)) "d"x` is
Choose the correct alternative:
`int secx/sqrt(cos2x) "d"x` is
Choose the correct alternative:
`int "e"^(- 7x) sin 5x "d"x` is
