Advertisements
Advertisements
प्रश्न
Given an arc of a circle, complete the circle.
उत्तर
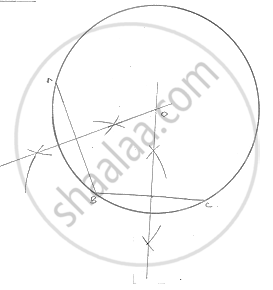
Steps of construction:
(i) Take three point A, B, C on the given Arc
(ii) Join AB and BC
(iii) Draw the perpendicular bisectors of chords AB and BC which interest each other at
point O, then O will required center of the required circle
(iv) Join OA
(v) With center O and radius OA, complete the circle
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
Segment of a circle is the region between an arc and .................. of the circle.
If O is the centre of the circle, find the value of x in the following figure

O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
In the given figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.
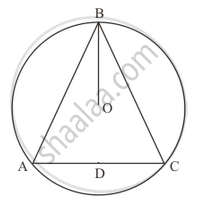
Prove that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half the hypotenuse.
If the given figure, AOC is a diameter of the circle and arc AXB = \[\frac{1}{2}\] arc BYC. Find ∠BOC.
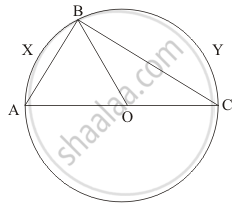
If arcs AXB and CYD of a circle are congruent, find the ratio of AB and CD.
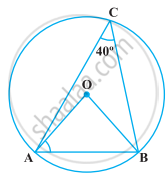
In the following figure, ∠ACB = 40º. Find ∠OAB.
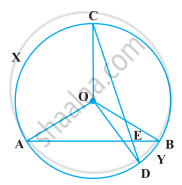
In the following figure, AB and CD are two chords of a circle intersecting each other at point E. Prove that ∠AEC = `1/2` (Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre).
A circle has radius `sqrt(2)` cm. It is divided into two segments by a chord of length 2 cm. Prove that the angle subtended by the chord at a point in major segment is 45°.
