Advertisements
Advertisements
प्रश्न
How many time constants will elapse before the energy stored in the capacitor reaches half of its equilibrium value in a charging RC circuit?
उत्तर
The equilibrium value of energy in a capacitor,
\[U = \frac{1}{2}\frac{Q^2}{C},\] where Q is the steady state charge.
Let q be the charge for which energy reaches half its equilibrium. Then,
\[\frac{1}{2}\frac{q^2}{C} = \frac{1}{2}U\]
\[ \Rightarrow \frac{1}{2}\frac{q^2}{C} = \frac{1}{2}\left( \frac{1}{2}\frac{Q^2}{C} \right)\]
\[ \Rightarrow q = \sqrt{\frac{Q^2}{2}}\]
The growth of charge in a capacitor,
\[q = Q\left( 1 - e^{- \frac{t}{RC}} \right)\]
\[ \because q = \sqrt{\frac{Q^2}{2} ,}\]
\[ \sqrt{\frac{Q^2}{2}} = Q\left( 1 - e^{- \frac{t}{RC}} \right)\]
\[ \Rightarrow \frac{Q}{\sqrt{2}} = Q\left( 1 - e^{- \frac{t}{RC}} \right)\]
\[ \Rightarrow e^{- \frac{t}{RC}} = \left( 1 - \frac{1}{\sqrt{2}} \right)\]
\[ \Rightarrow - \frac{t}{RC} = \ln\left( 1 - \frac{1}{\sqrt{2}} \right)\]
Let t = nRC
\[So, - \frac{nRC}{RC} = \ln\left( 1 - \frac{1}{\sqrt{2}} \right)\]
\[ \Rightarrow n = 1 . 23\]
APPEARS IN
संबंधित प्रश्न
Explain what would happen if the capacitor given in previous question a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
- While the voltage supply remained connected.
- After the supply was disconnected.
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
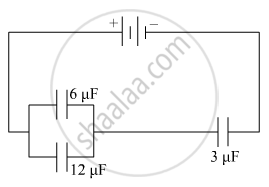
In the following arrangement of capacitors, the energy stored in the 6 µF capacitor is E. Find the value of the following :
(i) Energy stored in 12 µF capacitor.
(ii) Energy stored in 3 µF capacitor.
(iii) Total energy drawn from the battery.
Find the ratio of energy stored in the two configurations if they are both connected to the same source.
Find the charge on the capacitor shown in the figure.
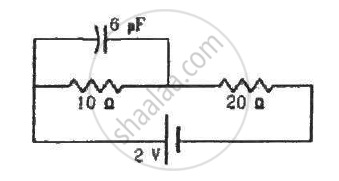
A 20 μF capacitor is joined to a battery of emf 6.0 V through a resistance of 100 Ω. Find the charge on the capacitor 2.0 ms after the connections are made.
A 100 μF capacitor is joined to a 24 V battery through a 1.0 MΩ resistor. Plot qualitative graphs (a) between current and time for the first 10 minutes and (b) between charge and time for the same period.
How many time constants will elapse before the current in a charging RC circuit drops to half of its initial value? Answer the same question for a discharging RC circuit.
Two capacitors of capacitances 4⋅0 µF and 6⋅0 µF are connected in series with a battery of 20 V. Find the energy supplied by the battery.
A capacitor of capacitance C is connected to a battery of emf ε at t = 0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate have this maximum value?
By evaluating ∫i2Rdt, show that when a capacitor is charged by connecting it to a battery through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
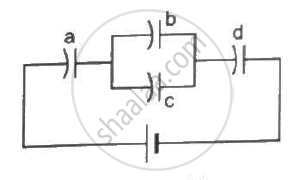
Each capacitor in figure has a capacitance of 10 µF. The emf of the battery is 100 V. Find the energy stored in each of the four capacitors.
A capacitor with stored energy 4⋅0 J is connected with an identical capacitor with no electric field in between. Find the total energy stored in the two capacitors.
A capacitor of capacitance C is given a charge Q. At t = 0, it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
A point charge Q is placed at the origin. Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
A large conducting plane has a surface charge density `1.0 xx 10^-4 "Cm"^-2` . Find the electrostatic energy stored in a cubical volume of edge 1⋅0 cm in front of the plane.
Answer the following question.
Obtain the expression for the energy stored in a capacitor connected across a dc battery. Hence define energy density of the capacitor
Choose the correct option:
Energy stored in a capacitor and dissipated during charging a capacitor bear a ratio.
If the p. d. across a capacitor is increased from 10 V to 30 V, then the energy stored with the capacitor ____________.
A parallel plate condenser is immersed in an oil of dielectric constant 2. The field between the plates is ______.
