Advertisements
Advertisements
प्रश्न
How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if
(i) 4 letters are used at a time,
(ii) all letters are used at a time,
(iii) all letters are used but first letter is a vowel?
उत्तर
There are 6 different letters in the word MONDAY.
(i) Number of 4-letter words that can be formed from the letters of the word MONDAY, without repetition of letters, is the number of permutations of 6 different objects taken 4 at a time, which is `""^6P_4`.
Thus, required number of words that can be formed using 4 letters at a time is
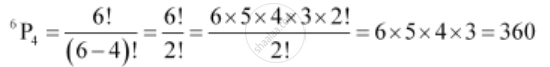
(ii) Number of words that can be formed by using all the letters of the word MONDAY at a time is the number of permutations of 6 different objects taken 6 at a time, which is `""^6P_6 = 6!`.
Thus, required number of words that can be formed when all letters are used at a time = 6! = 6 × 5 × 4 × 3 × 2 ×1 = 720
(iii) In the given word, there are 2 different vowels, which have to occupy the rightmost place of the words formed. This can be done only in 2 ways.
Since the letters cannot be repeated and the rightmost place is already occupied with a letter (which is a vowel), the remaining five places are to be filled by the remaining 5 letters. This can be done in 5! ways.
Thus, in this case, required number of words that can be formed is
5! × 2 = 120 × 2 = 240
APPEARS IN
संबंधित प्रश्न
Evaluate 4! – 3!
Evaluate `(n!)/((n-r)!)`, when n = 9, r = 5
How many 4-digit numbers are there with no digit repeated?
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?
In how many ways can the letters of the word PERMUTATIONS be arranged if the vowels are all together.
In how many ways can the letters of the word PERMUTATIONS be arranged if the there are always 4 letters between P and S?
How many natural numbers less than 1000 can be formed from the digits 0, 1, 2, 3, 4, 5 when a digit may be repeated any number of times?
Find the total number of ways in which 20 balls can be put into 5 boxes so that first box contains just one ball ?
In how many ways can 5 different balls be distributed among three boxes?
In how many ways can 4 prizes be distributed among 5 students, when
(i) no student gets more than one prize?
(ii) a student may get any number of prizes?
(iii) no student gets all the prizes?
The number of words that can be formed out of the letters of the word "ARTICLE" so that vowels occupy even places is
How many numbers greater than 10 lacs be formed from 2, 3, 0, 3, 4, 2, 3 ?
The number of ways in which the letters of the word 'CONSTANT' can be arranged without changing the relative positions of the vowels and consonants is
Number of all four digit numbers having different digits formed of the digits 1, 2, 3, 4 and 5 and divisible by 4 is
A 5-digit number divisible by 3 is to be formed using the digits 0, 1, 2, 3, 4 and 5 without repetition. The total number of ways in which this can be done is
If k + 5Pk + 1 =\[\frac{11 (k - 1)}{2}\]. k + 3Pk , then the values of k are
The number of words that can be made by re-arranging the letters of the word APURBA so that vowels and consonants are alternate is
English alphabet has 11 symmetric letters that appear same when looked at in a mirror. These letters are A, H, I, M, O, T, U, V, W, X and Y. How many symmetric three letters passwords can be formed using these letters?
Evaluate the following.
`(3! + 1!)/(2^2!)`
Determine the number of permutations of the letters of the word SIMPLE if all are taken at a time?
How many strings can be formed from the letters of the word ARTICLE, so that vowels occupy the even places?
In how many ways 4 mathematics books, 3 physics books, 2 chemistry books and 1 biology book can be arranged on a shelf so that all books of the same subjects are together
Each of the digits 1, 1, 2, 3, 3 and 4 is written on a separate card. The six cards are then laid out in a row to form a 6-digit number. How many distinct 6-digit numbers are there?
If the letters of the word GARDEN are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, then find the ranks of the words
GARDEN
If the letters of the word GARDEN are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, then find the ranks of the words
DANGER
Choose the correct alternative:
If Pr stands for rPr then the sum of the series 1 + P1 + 2P2 + 3P3 + · · · + nPn is
Suppose m men and n women are to be seated in a row so that no two women sit together. If m > n, show that the number of ways in which they can be seated is `(m!(m + 1)!)/((m - n + 1)1)`
There are 10 persons named P1, P2, P3, ... P10. Out of 10 persons, 5 persons are to be arranged in a line such that in each arrangement P1 must occur whereas P4 and P5 do not occur. Find the number of such possible arrangements.
The number of words which can be formed out of the letters of the word ARTICLE, so that vowels occupy the even place is ______.
In the permutations of n things, r taken together, the number of permutations in which m particular things occur together is `""^(n - m)"P"_(r - m) xx ""^r"P"_m`.
Five boys and five girls form a line. Find the number of ways of making the seating arrangement under the following condition:
| C1 | C2 |
| (a) Boys and girls alternate: | (i) 5! × 6! |
| (b) No two girls sit together : | (ii) 10! – 5! 6! |
| (c) All the girls sit together | (iii) (5!)2 + (5!)2 |
| (d) All the girls are never together : | (iv) 2! 5! 5! |
How many words (with or without dictionary meaning) can be made from the letters of the word MONDAY, assuming that no letter is repeated, if
| C1 | C2 |
| (a) 4 letters are used at a time | (i) 720 |
| (b) All letters are used at a time | (ii) 240 |
| (c) All letters are used but the first is a vowel | (iii) 360 |
The number of three-digit even numbers, formed by the digits 0, 1, 3, 4, 6, 7 if the repetition of digits is not allowed, is ______.
The number of permutations by taking all letters and keeping the vowels of the word ‘COMBINE’ in the odd places is ______.
