Advertisements
Advertisements
प्रश्न
How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if
(i) 4 letters are used at a time,
(ii) all letters are used at a time,
(iii) all letters are used but first letter is a vowel?
उत्तर
There are 6 different letters in the word MONDAY.
(i) Number of 4-letter words that can be formed from the letters of the word MONDAY, without repetition of letters, is the number of permutations of 6 different objects taken 4 at a time, which is `""^6P_4`.
Thus, required number of words that can be formed using 4 letters at a time is
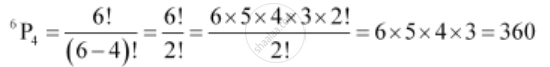
(ii) Number of words that can be formed by using all the letters of the word MONDAY at a time is the number of permutations of 6 different objects taken 6 at a time, which is `""^6P_6 = 6!`.
Thus, required number of words that can be formed when all letters are used at a time = 6! = 6 × 5 × 4 × 3 × 2 ×1 = 720
(iii) In the given word, there are 2 different vowels, which have to occupy the rightmost place of the words formed. This can be done only in 2 ways.
Since the letters cannot be repeated and the rightmost place is already occupied with a letter (which is a vowel), the remaining five places are to be filled by the remaining 5 letters. This can be done in 5! ways.
Thus, in this case, required number of words that can be formed is
5! × 2 = 120 × 2 = 240
APPEARS IN
संबंधित प्रश्न
Is 3! + 4! = 7!?
How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
Find n if n – 1P3 : nP4 = 1 : 9
Find r if `""^5P_r = 2^6 P_(r-1)`
Find r if `""^5P_r = ""^6P_(r-1)`
In how many ways can the letters of the word PERMUTATIONS be arranged if the words start with P and end with S.
Find x in each of the following:
In how many ways can three jobs I, II and III be assigned to three persons A, B and C if one person is assigned only one job and all are capable of doing each job?
If three six faced die each marked with numbers 1 to 6 on six faces, are thrown find the total number of possible outcomes ?
How many three digit numbers can be formed by using the digits 0, 1, 3, 5, 7 while each digit may be repeated any number of times?
Three dice are rolled. Find the number of possible outcomes in which at least one die shows 5 ?
In how many ways can 4 letters be posted in 5 letter boxes?
Write the total number of possible outcomes in a throw of 3 dice in which at least one of the dice shows an even number.
Write the number of ways in which 7 men and 7 women can sit on a round table such that no two women sit together ?
Write the number of words that can be formed out of the letters of the word 'COMMITTEE' ?
Write the number of numbers that can be formed using all for digits 1, 2, 3, 4 ?
The number of different signals which can be given from 6 flags of different colours taking one or more at a time, is
If the letters of the word KRISNA are arranged in all possible ways and these words are written out as in a dictionary, then the rank of the word KRISNA is
In how many ways 5 boys and 3 girls can be seated in a row, so that no two girls are together?
- In how many ways can 8 identical beads be strung on a necklace?
- In how many ways can 8 boys form a ring?
Find the rank of the word ‘CHAT’ in the dictionary.
Evaluate the following.
`(3! xx 0! + 0!)/(2!)`
The possible outcomes when a coin is tossed five times:
If n is a positive integer, then the number of terms in the expansion of (x + a)n is:
The total number of 9 digit number which has all different digit is:
The number of words with or without meaning that can be formed using letters of the word “EQUATION”, with no repetition of letters is:
The number of permutation of n different things taken r at a time, when the repetition is allowed is:
A test consists of 10 multiple choice questions. In how many ways can the test be answered if question number n has n + 1 choices?
A student appears in an objective test which contain 5 multiple choice questions. Each question has four choices out of which one correct answer.
What is the maximum number of different answers can the students give?
In how many ways 4 mathematics books, 3 physics books, 2 chemistry books and 1 biology book can be arranged on a shelf so that all books of the same subjects are together
How many strings are there using the letters of the word INTERMEDIATE, if no two vowels are together
If the letters of the word GARDEN are permuted in all possible ways and the strings thus formed are arranged in the dictionary order, then find the ranks of the words
DANGER
Three married couples are to be seated in a row having six seats in a cinema hall. If spouses are to be seated next to each other, in how many ways can they be seated? Find also the number of ways of their seating if all the ladies sit together.
Find the number of different words that can be formed from the letters of the word ‘TRIANGLE’ so that no vowels are together
A five-digit number divisible by 3 is to be formed using the numbers 0, 1, 2, 3, 4 and 5 without repetitions. The total number of ways this can be done is ______.
8-digit numbers are formed using the digits 1, 1, 2, 2, 2, 3, 4, 4. The number of such numbers in which the odd digits do no occupy odd places is ______.
The number of permutations by taking all letters and keeping the vowels of the word ‘COMBINE’ in the odd places is ______.
