Advertisements
Advertisements
प्रश्न
Identify the unit vector in the following.
विकल्प
`hati + hatj`
`hati/sqrt2`
`hatk - hatj/sqrt2`
`(hati + hatj)/sqrt2`
उत्तर
`underline((hati + hatj)/sqrt2)`
APPEARS IN
संबंधित प्रश्न
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = -hati + hatj - hatk`, find the unit vector in the direction of the vector `veca +vecb`.
The position vector particle has a length of 1m and makes 30° with the x-axis. What are the lengths of the x and y components of the position vector?
Compare the components for the following vector equations
(a) `"T"hatj - "mg"hatj = "ma"hatj`
(b) `vecT + vecF = vecA + vecB`
(c) `vecT - vecF = vecA - vecB`
(d) `"T"hatj + "mg"hatj = "ma"hatj`
If `overlinea`, `overlineb` and `overlinec` are three non-coplanar vectors then `(overlinea + overlineb + overlinec).[(overlinea + overlineb) xx (overlinea + overlinec)]` = ______
If `overline(a),overline(b),overline(c)` are non-coplanar vectors and λ is a real number then `[lambda(overline(a)+overline(b))lambda^2overline(b) lambda overline(c)]=[overline(a) overline(b)+overline(c) overline(b)]` for ______.
Find the vector component of the vector with initial point (2, 1) and terminal point (–5, 7).
Unit vector perpendicular to the plane of the triangle ABC with position vectors `veca, vecb, vecc` of the vertices A, B, C is ______.
If `veca = 4hati + 6hatj` and `vecb = 3hatj + 4hatk`, then the vector form of the component of `veca` along `vecb` is ______.
Check whether the vectors `2hati + 2hatj +3hatk, -3hati +3hatj +2hatk` and `3hati +4hatk` form a triangle or not.
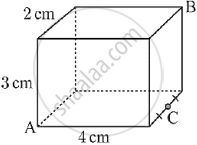
Shown below is a cuboid. Find `vec(BA).vec(BC)`