Advertisements
Advertisements
प्रश्न
Identify the unit vector in the following.
पर्याय
`hati + hatj`
`hati/sqrt2`
`hatk - hatj/sqrt2`
`(hati + hatj)/sqrt2`
उत्तर
`underline((hati + hatj)/sqrt2)`
APPEARS IN
संबंधित प्रश्न
Write the number of vectors of unit length perpendicular to both the vectors `veca=2hati+hatj+2hatk and vecb=hatj+hatk`
If `veca=4hati-hatj+hatk` then find a unit vector parallel to the vector `veca+vecb`
Show that the direction cosines of a vector equally inclined to the axes OX, OY, and OZ are `pm1/sqrt3, 1/sqrt3, 1/sqrt3`.
The position vector particle has a length of 1m and makes 30° with the x-axis. What are the lengths of the x and y components of the position vector?
If `overline(a),overline(b),overline(c)` are non-coplanar vectors and λ is a real number then `[lambda(overline(a)+overline(b))lambda^2overline(b) lambda overline(c)]=[overline(a) overline(b)+overline(c) overline(b)]` for ______.
If the horizontal and vertical components of a force are negative, then that force is acting in between
If a line makes angles 120° and 60° with the positive directions of X and Z axes respectively then the angle made by the line with positive Y-axis is ______.
Two vectors `veca = a_1 hati + a_2 hatj + a_3 hatk` and `vecb = b_1 hati + b_2 hatj + b_3 hatk` are collinear if ______.
If `veca = 3hati - 2hatj + hatk` and `vecb = 2hati - 4hatj - 3hatk` then the value of `|veca - 2vecb|` will be ______.
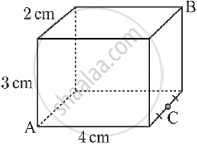
Shown below is a cuboid. Find `vec(BA).vec(BC)`