Advertisements
Advertisements
प्रश्न
Show that the direction cosines of a vector equally inclined to the axes OX, OY, and OZ are `pm1/sqrt3, 1/sqrt3, 1/sqrt3`.
उत्तर
The direction ratio are < 1, 1, 1>
∴ Direction cosines are
`<1/sqrt (1 + 1 + 1), 1/sqrt(1 + 1 + 1), 1/ sqrt(1 + 1 + 1)>`
i.e., `< 1/sqrt3, 1/sqrt3, 1/sqrt3>`
APPEARS IN
संबंधित प्रश्न
Write the number of vectors of unit length perpendicular to both the vectors `veca=2hati+hatj+2hatk and vecb=hatj+hatk`
If `veca=4hati-hatj+hatk` then find a unit vector parallel to the vector `veca+vecb`
For given vectors, `veca = 2hati - hatj + 2hatk` and `vecb = -hati + hatj - hatk`, find the unit vector in the direction of the vector `veca +vecb`.
Find a vector in the direction of vector `5hati - hatj +2hatk` which has a magnitude of 8 units.
Identify the unit vector in the following.
How do you deduce that two vectors are perpendicular?
The position vector particle has a length of 1m and makes 30° with the x-axis. What are the lengths of the x and y components of the position vector?
Compare the components for the following vector equations
(a) `"T"hatj - "mg"hatj = "ma"hatj`
(b) `vecT + vecF = vecA + vecB`
(c) `vecT - vecF = vecA - vecB`
(d) `"T"hatj + "mg"hatj = "ma"hatj`
If `overlinea`, `overlineb` and `overlinec` are three non-coplanar vectors then `(overlinea + overlineb + overlinec).[(overlinea + overlineb) xx (overlinea + overlinec)]` = ______
If `overline(a),overline(b),overline(c)` are non-coplanar vectors and λ is a real number then `[lambda(overline(a)+overline(b))lambda^2overline(b) lambda overline(c)]=[overline(a) overline(b)+overline(c) overline(b)]` for ______.
If the horizontal and vertical components of a force are negative, then that force is acting in between
Unit vector perpendicular to the plane of the triangle ABC with position vectors `veca, vecb, vecc` of the vertices A, B, C is ______.
If a line makes angles 120° and 60° with the positive directions of X and Z axes respectively then the angle made by the line with positive Y-axis is ______.
Two vectors `veca = a_1 hati + a_2 hatj + a_3 hatk` and `vecb = b_1 hati + b_2 hatj + b_3 hatk` are collinear if ______.
If `veca = 4hati + 6hatj` and `vecb = 3hatj + 4hatk`, then the vector form of the component of `veca` along `vecb` is ______.
If `4hati - 5hatj + hatk, 2hati + 3hatj + 3hatk` and `xhati + yhatj + zhatk` represent the sides AB, BC and AC respectively of a triangle ABC, then find x, y, z.
Check whether the vectors `2hati + 2hatj +3hatk, -3hati +3hatj +2hatk` and `3hati +4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj+ 3hatk`, `-3hati + 3hatj +2hatk` and `3hati + 4hatk` form a triangle or not.
If `veca = 3hati - 2hatj + hatk` and `vecb = 2hati - 4hatj - 3hatk` then the value of `|veca - 2vecb|` will be ______.
Shown below is a cuboid. Find `vec(BA).vec(BC)`
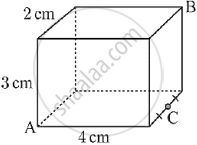
Check whether the vectors `2hati + 2hatj + 3hatk , -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
