Question

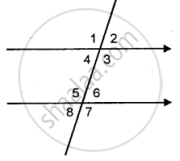
If ∠1 = 120°, find the measures of : ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8. Give reasons.

Answer 1

l || m and p is their transversal and ∠1 = 120°

∠1 + ∠2 = 180°    (Straight line angle)

∴ 120° + ∠2 = 180°

⇒ ∠2 = 180° - 120° = 60°

∴ ∠2 = 60°

But ∠1 = ∠3   (Vertically opposite angles)

∴ ∠3 = ∠1 = 120°

Similarly ∠4 = ∠2   (Vertically opposite angles)

∴ ∠4 = 60°

∠5 = ∠1     (Corresponding angles)

∴ ∠5 = 120°

Similarly ∠6 = ∠2   (Corresponding angles)

∴ ∠6 = 60°

∠7 = ∠5   (Vertically opposite angles)

∴  ∠7 = 120°

and ∠8 = ∠6 (Vertically opposite angles)

∴  ∠8 = 60°

Hence ∠2 = 60°, ∠3 = 120°, ∠4 = 60°,∠5 = 120°, ∠6 = 60°, ∠7 = 120° and ∠8 = 60°.