Advertisements
Advertisements
Question
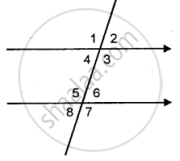
If ∠1 = 120°, find the measures of : ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8. Give reasons.
Solution
l || m and p is their transversal and ∠1 = 120°
∠1 + ∠2 = 180° (Straight line angle)
∴ 120° + ∠2 = 180°
⇒ ∠2 = 180° - 120° = 60°
∴ ∠2 = 60°
But ∠1 = ∠3 (Vertically opposite angles)
∴ ∠3 = ∠1 = 120°
Similarly ∠4 = ∠2 (Vertically opposite angles)
∴ ∠4 = 60°
∠5 = ∠1 (Corresponding angles)
∴ ∠5 = 120°
Similarly ∠6 = ∠2 (Corresponding angles)
∴ ∠6 = 60°
∠7 = ∠5 (Vertically opposite angles)
∴ ∠7 = 120°
and ∠8 = ∠6 (Vertically opposite angles)
∴ ∠8 = 60°
Hence ∠2 = 60°, ∠3 = 120°, ∠4 = 60°,∠5 = 120°, ∠6 = 60°, ∠7 = 120° and ∠8 = 60°.
APPEARS IN
RELATED QUESTIONS
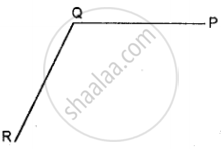
In your note-book copy the following angle using ruler and a pair compass only.
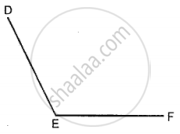
In your note-book copy the following angle using ruler and a pair compass only.
Construct the 135° angle, using ruler and a pair of compass only.
Construct the 15° angle, using ruler and a pair of compass only.
Draw a line segment PQ = 8cm. Construct the perpendicular bisector of the line segment PQ. Let the perpendicular bisector drawn meet PQ at point R. Measure the lengths of PR and QR. Is PR = QR?
Draw a line segment OA = 5 cm. Use set-square to construct angle AOB = 60°, such that OB = 3 cm. Join A and B; then measure the length of AB.
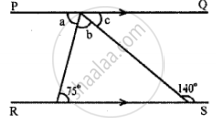
In the following figures, PQ is parallel to RS. Find the angles a, b and c:
Two straight lines are cut by a transversal so that the co-interior angles are equal. What must be the measure of each interior angle to make the straight lines parallel to each other?
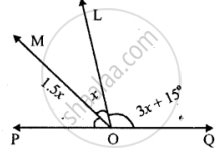
In the case given below, find the value of x so that POQ is straight line
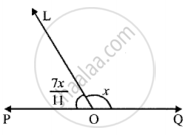
In the case given below, find the value of x so that POQ is straight line