Advertisements
Advertisements
प्रश्न
If 69.5 is the mean of 72, 70, ‘x’, 62, 50, 71, 90, 64, 58 and 82, find the value of ‘x’.
उत्तर
No. of terms = 10
Mean = 69.5
Sum of the numbers = 69.5 × 10 = 695 ...(i)
But sum of numbers = 72 + 70 + x + 62 + 50 + 71 + 90 + 64 + 58 + 82 = 619 + x ...(ii)
From (i) and (ii)
619 + x = 695
`\implies` x = 695 – 619
`\implies` x = 76
APPEARS IN
संबंधित प्रश्न
Using the information given in the adjoining histogram, calculate the mean.
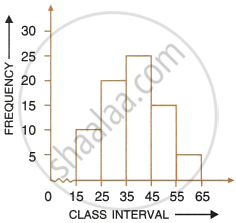
Q 11
The data on the number of patients attending a hospital in a month are given below. Find the average (mean) number of patients attending the hospital in a month by using the shortcut method. Take the assumed mean as 45. Give your answer correct to 2 decimal places.
| Number of patients | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 |
| Number of Days | 5 | 2 | 7 | 9 | 2 | 5 |
In a basket there are 10 tomatoes. The weight of each of these tomatoes in grams is as follows:
60, 70, 90, 95, 50, 65, 70, 80, 85, 95.
Find the median of the weights of tomatoes.
The heights of 9 persons are 142 cm, 158 cm, 152 cm, 143 cm, 139 cm, 144 cm, 146 cm, 148 cm and 151 cm. Find the mean height.
Find the mode of the following frequency distribution:
| Hrs. Spent daily in studies | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 |
| No. of students | 8 | 7 | 3 | 5 | 10 | 6 | 3 | 4 |
The percentage marks obtained in 10 subjects by a student are 84, 88, 72, 91, 68, 75, 98, 96, 79 and 86. Find the median of the marks obtained.
Estimate the median, the lower quartile and the upper quartile of the following frequency distribution by drawing an ogive:
| Age( in yrs) | Under 10 | Under 20 | Under 30 | Under 40 | Under 50 | Under 60 |
| No. of males | 6 | 10 | 25 | 32 | 43 | 50 |
Find the median of:
63, 17, 50, 9, 25, 43, 21, 50, 14 and 34
Find the median of 25, 16, 15, 10, 8, 30
