Advertisements
Advertisements
प्रश्न
If A and B are (−2, −2) and (2, −4), respectively, find the coordinates of P such that `"AP" = 3/7 "AB"` and P lies on the line segment AB.
उत्तर १

The coordinates of point A and B are (−2, −2) and (2, −4) respectively.
Since AP = `3/7 "AB"`
Therefore, AP: PB = 3:4
Point P divides the line segment AB in the ratio 3:4.
Coordinates of P = `((3xx2+4xx(-2))/(3+4), (3xx(-4)+4xx(-2))/(3+4))`
= `((6-8)/7, (-12-8)/7)`
= `(-2/7, -20/7)`
उत्तर २
We have two points A (-2, -2) and B (2, -4). Let P be any point which divides AB as
`"AP" = 3/7 "AB"`
Since,
AB = (AP + BP)
So,
7AP = 3AB
7AP = 3(AP + BP)
4AP = 3BP
`("AP")/("BP") = 3/4`
Now according to the section formula if any point P divides a line segment joining A(x1, y1) and B(x2, y2) in the ratio m: n internally than,
P(x, y) = `((nx_1 + mx_2)/(m + n)"," (ny_1 + my_2)/(m + n))`
Therefore, P divides AB in the ratio 3: 4. So,
P(x, y) = `((3(2) + 4(-2))/(3 + 4)"," (3(-4) + 4(-2))/(3 + 4))`
= `(-2/7,-20/7)`
APPEARS IN
संबंधित प्रश्न
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) such that AP =(2/5)AB.
Find the lengths of the medians of a ∆ABC whose vertices are A(7, –3), B(5,3) and C(3,–1)
Find the coordinates of the centroid of a triangle whose vertices are (–1, 0), (5, –2) and (8, 2)
If the coordinates of the mid points of the sides of a triangle are (1, 1), (2, – 3) and (3, 4) Find its centroid
Find the ratio in which P(4, m) divides the line segment joining the points A(2, 3) and B(6, –3). Hence find m.
The line segment joining the points (3, -4) and (1, 2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and (5/3, q) respectively. Find the values of p and q.
If A and B are two points having coordinates (−2, −2) and (2, −4) respectively, find the coordinates of P such that `AP = 3/7 AB`
Show that the line segment joining the points (–5, 8) and (10, −4) is trisected by the co-ordinate axes.
Given a line segment AB joining the points A(−4, 6) and B(8, −3). Find:
- the ratio in which AB is divided by the y-axis.
- find the coordinates of the point of intersection.
- the length of AB.
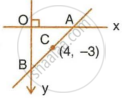
The mid-point of the segment AB, as shown in diagram, is C(4, –3). Write down the co-ordinates of A and B.
Find the length of the hypotenuse of a square whose side is 16 cm.
Find the coordinate of a point P which divides the line segment joining :
5(2, 6) and R(9, -8) in the ratio 3: 4.
Find the ratio in which the line y = -1 divides the line segment joining (6, 5) and (-2, -11). Find the coordinates of the point of intersection.
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
If point P(1, 1) divide segment joining point A and point B(–1, –1) in the ratio 5 : 2, then the coordinates of A are ______
Point P(– 4, 6) divides point A(– 6, 10) and B(m, n) in the ratio 2:1, then find the coordinates of point B
The line segment joining the points A(3, 2) and B(5, 1) is divided at the point P in the ratio 1 : 2 and it lies on the line 3x – 18y + k = 0. Find the value of k.
Complete the following activity to find the coordinates of point P which divides seg AB in the ratio 3:1 where A(4, – 3) and B(8, 5).
Activity:
∴ By section formula,
∴ x = `("m"x_2 + "n"x_1)/square`,
∴ x = `(3 xx 8 + 1 xx 4)/(3 + 1)`,
= `(square + 4)/4`,
∴ x = `square`,
∴ y = `square/("m" + "n")`
∴ y = `(3 xx 5 + 1 xx (-3))/(3 + 1)`
= `(square - 3)/4`
∴ y = `square`
