Advertisements
Advertisements
प्रश्न
If point P(1, 1) divide segment joining point A and point B(–1, –1) in the ratio 5 : 2, then the coordinates of A are ______
विकल्प
(3, 3)
(6, 6)
(2, 2)
(1, 1)
उत्तर
(6, 6)
Let A(x1, y1) and B(x2, y2) = B(-1, -1)
P(x, y) = P(1, 1) divides AB in ratio 5 : 2.
∴ x1 = 1, y1 = 1, x2 = –1, y2 = –1, a = 5, b = 2.
∴ By section formula,
∴ x = `(ax_2 + bx_1)/(a + b)`
∴ `1 = (5(-1) + 2x_1)/(5 + 2)`
∴ 7 = -5 + 2x1
∴ 2x1 = 7 + 5
∴ 2x1 = 12
∴ x1 = `12/2`
∴ x1 = 6
∴ Co-ordinates of A are (6, 6).
संबंधित प्रश्न
Find the coordinates of points which trisect the line segment joining (1, –2) and (–3, 4)
Prove that the points (–2, –1), (1, 0), (4, 3) and (1, 2) are the vertices of a parallelogram. Is it a rectangle ?
If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (-2,-3) and (5 2) find the other vertices.
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
The line joining the points A (–3, –10) and B (–2, 6) is divided by the point P such that `(PB)/(AB) = 1/5`. Find the co-ordinates of P.
Calculate the ratio in which the line joining the points (–3, –1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
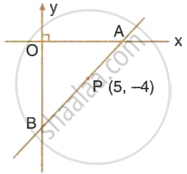
The point P (5, – 4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B. Given AP is smaller than BP.
The line segment joining the points M(5, 7) and N(–3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
The line segment joining A (2, 3) and B (6, –5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K.
The line joining P(–4, 5) and Q(3, 2) intersects the y-axis at point R. PM and QN are perpendicular from P and Q on the x-axis Find:
- the ratio PR : RQ
- the coordinates of R.
- the area of the quadrilateral PMNQ.
Find the co-ordinates of the centroid of a triangle ABC whose vertices are: A(–1, 3), B(1, –1) and C(5, 1).
If two adjacent vertices of a parallelogram are (3, 2) and (−1, 0) and the diagonals intersect at (2, −5), then find the coordinates of the other two vertices.
A (30, 20) and B ( 6, -4) are two fixed points. Find the coordinates of a point Pin AB such that 2PB = AP. Also, find the coordinates of some other point Qin AB such that AB = 6 AQ.
Find the ratio in which the line segment joining P ( 4, -6) and Q ( -3, 8) is divided by the line y = 0.
In what ratio is the line joining (2, -1) and (-5, 6) divided by the y axis ?
Point P(– 4, 6) divides point A(– 6, 10) and B(m, n) in the ratio 2:1, then find the coordinates of point B
If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5) and R(-2, 3), then the value of ‘a’ is ______.
The vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6) and D(3, 5). Then (x, y) is ______.
If P(9a – 2, – b) divides line segment joining A(3a + 1, –3) and B(8a, 5) in the ratio 3 : 1, find the values of a and b.
Find the ratio in which the x-axis divides internally the line joining points A (6, -4) and B ( -3, 8).
