Advertisements
Advertisements
प्रश्न
If a train runs at 60 km/hr it reaches its destination late by 15 minutes. But, if it runs at 85 kmph it is late by only 4 minutes. Find the distance to be covered by the train.
उत्तर
Let the distance to be covered by train be ‘d’
Using the formula, time take (t) = `"Distance"/"Speed"`
Case 1:
If speed = 60km/h
The time taken is 15 minutes more than usual `("t" + 15/60)`
Let the usual time taken be ‘t’ hrs.
Caution: Since speed is given in km/hr, we should take care to maintain all units such as time should be in hour and distance should be in min.
Given that in case 1, it takes 15 min. more
15 m = `15/60` hr
= `1/4` hr
∴ Substituting in formula,
∴ `"d"/60 = "t" + 1/4`
Since usually it takes ‘t’ hr, but when running at 60 k, it kes 15 min `(1/4 "hr")` extra
Multiplying by 60 on both sides
d = `60 xx "t" + 60 xx 1/4`
60t + 15 ...(1)
Case 2:
Speed is given as 85 km/h
Time taken is only 4 min `(4/60 "hr")` more than usual time
∴ time taken = `("t" + 1/35) "hr". (4/60 = 1/15)`
Using the formula,
`"Distance"/"Speed"` = time
Multiplying by 85 on both sides
`"d"/85 xx 85 = 85 xx "t" + 85 xx 1/15`
∴ d = `85"t" + 17/3` ...(2)
From (1) and (2), we will solve for ‘r’
Equating and eliminating ‘d’ we get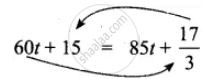
∴ By transposing, we get
`15 - 17/3` = 85t − 60t
`(45 - 17)/3` = 25t
∴ 25t = `28/3`
∴ t = `28/(3 xx 25)`
= `28/75` hr ...`(28/75 xx 60 = 22.4 "min")`
Substituting this value of ‘t’ in eqn. (1), we get
d = 60t + 15
= `60 xx 28/75 + 15`
= `1680/75 + 15`
= 22.4 + 15
= 37.4 km
APPEARS IN
संबंधित प्रश्न
Find x and m: `("m" + 9)/(3"m" + 15) = 5/3`
x = 25 is the solution of one third of a number is less than 10 the original number.
The product of L.C.M and H.C.F of two numbers is 24. If one of the number is 6, then the other number is ________
If ‘g’ is equal to 300 what is the value of ‘g – 1’ and ‘g + 1’?
Gopal is 8 years younger to Karnan. If the sum of their ages is 30, how old is Karnan?
The solution of the equation `2y = 5y - 18/5` is ______.
Which of the following equations does not have a solution in integers?
In the equation 7k – 7 = 7, the variable is 7.
Translate the following statements into an equation:
The perimeter (p) of an equilateral triangle is three times of its side (a).
Finding the value of a variable in a linear equation that ______ the equation is called a ______ of the equation.
