Advertisements
Advertisements
प्रश्न
The denominator of a fraction exceeds Its numerator by 8. If the numerator is increased by 17 and the denominator is decreased by 1, we get `3/2`. Find the original fraction.
Advertisements
उत्तर
Let the numerator & denominator be ‘n’ & ‘d’
Given that denominator exceeds numerator by 8
∴ d = n + 8 ...(1)
If numerator increased by 17 & denominator decreased by 1,
it becomes (n + 17) & (d – 1), fraction is `3/2`
i.e `("n" + 17)/("d" - 1) = 3/2` by cross multiplying, we get
`("n" + 17)/("d" - 1) = 3/2`
2(n + 17) = 3(d – 1)
2n + 2 × 17 = 3d – 3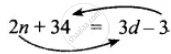
∴ 34 + 3 = 3d – 2n
∴ 3d – 2n = 37 ...(2)
Substituting equation (1) in (2), we get,
3 × (n + 8) – 2n = 37
3n + 3 × 8 – 2n = 37
∴ n = 37 – 24 = 13
d = n + 8 = 13 + 8 = 21
The fraction is `"n"/"d" = 13/21`
APPEARS IN
संबंधित प्रश्न
Divide the given polynomial by the given monomial.
(5x2 − 6x) ÷ 3x
Which of the following expressions are not polynomials?
Divide 6x3y2z2 by 3x2yz.
Verify the division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following. Also, write the quotient and remainder.
| Dividend | Divisor |
| 15y4 − 16y3 + 9y2 −\[\frac{10}{3}\] y+6 | 3y − 2 |
Using division of polynomials, state whether
2y − 5 is a factor of 4y4 − 10y3 − 10y2 + 30y − 15
Using division of polynomials, state whether
3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y − 35
Using division of polynomials, state whether
z2 + 3 is a factor of z5 − 9z
Divide the first polynomial by the second in each of the following. Also, write the quotient and remainder:
5y3 − 6y2 + 6y − 1, 5y − 1
Divide 24(x2yz + xy2z + xyz2) by 8xyz using both the methods.
Divide 27y3 by 3y
