Advertisements
Advertisements
प्रश्न
If a train runs at 60 km/hr it reaches its destination late by 15 minutes. But, if it runs at 85 kmph it is late by only 4 minutes. Find the distance to be covered by the train.
उत्तर
Let the distance to be covered by train be ‘d’
Using the formula, time take (t) = `"Distance"/"Speed"`
Case 1:
If speed = 60km/h
The time taken is 15 minutes more than usual `("t" + 15/60)`
Let the usual time taken be ‘t’ hrs.
Caution: Since speed is given in km/hr, we should take care to maintain all units such as time should be in hour and distance should be in min.
Given that in case 1, it takes 15 min. more
15 m = `15/60` hr
= `1/4` hr
∴ Substituting in formula,
∴ `"d"/60 = "t" + 1/4`
Since usually it takes ‘t’ hr, but when running at 60 k, it kes 15 min `(1/4 "hr")` extra
Multiplying by 60 on both sides
d = `60 xx "t" + 60 xx 1/4`
60t + 15 ...(1)
Case 2:
Speed is given as 85 km/h
Time taken is only 4 min `(4/60 "hr")` more than usual time
∴ time taken = `("t" + 1/35) "hr". (4/60 = 1/15)`
Using the formula,
`"Distance"/"Speed"` = time
Multiplying by 85 on both sides
`"d"/85 xx 85 = 85 xx "t" + 85 xx 1/15`
∴ d = `85"t" + 17/3` ...(2)
From (1) and (2), we will solve for ‘r’
Equating and eliminating ‘d’ we get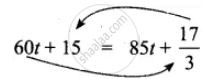
∴ By transposing, we get
`15 - 17/3` = 85t − 60t
`(45 - 17)/3` = 25t
∴ 25t = `28/3`
∴ t = `28/(3 xx 25)`
= `28/75` hr ...`(28/75 xx 60 = 22.4 "min")`
Substituting this value of ‘t’ in eqn. (1), we get
d = 60t + 15
= `60 xx 28/75 + 15`
= `1680/75 + 15`
= 22.4 + 15
= 37.4 km
APPEARS IN
संबंधित प्रश्न
If a and b are positive integers then the solution of the equation ax = b has to be always _______
A number consists of two digits whose sum is 9. If 27 is subtracted from the original number, its digits are interchanged. Find the original number
The taxi charges in a city comprised of a fixed charge of ₹ 100 for 5 kms and ₹ 16 per km for every additional km. If the amount paid at the end of the trip was ₹ 740 find the distance travelled.
If ‘p − 5’ gives 12 then ‘p’ is _____________
The solution of which of the following equations is neither a fraction nor an integer.
If a and b are positive integers, then the solution of the equation ax = b has to be always ______.
The solution of the equation 3x – 4 = 1 – 2x is ______.
The solution of the equation `2y = 5y - 18/5` is ______.
0 is a solution of the equation x + 1 = 0.
In an equation, the LHS is equal to the RHS.
