Advertisements
Advertisements
Question
If a train runs at 60 km/hr it reaches its destination late by 15 minutes. But, if it runs at 85 kmph it is late by only 4 minutes. Find the distance to be covered by the train.
Solution
Let the distance to be covered by train be ‘d’
Using the formula, time take (t) = `"Distance"/"Speed"`
Case 1:
If speed = 60km/h
The time taken is 15 minutes more than usual `("t" + 15/60)`
Let the usual time taken be ‘t’ hrs.
Caution: Since speed is given in km/hr, we should take care to maintain all units such as time should be in hour and distance should be in min.
Given that in case 1, it takes 15 min. more
15 m = `15/60` hr
= `1/4` hr
∴ Substituting in formula,
∴ `"d"/60 = "t" + 1/4`
Since usually it takes ‘t’ hr, but when running at 60 k, it kes 15 min `(1/4 "hr")` extra
Multiplying by 60 on both sides
d = `60 xx "t" + 60 xx 1/4`
60t + 15 ...(1)
Case 2:
Speed is given as 85 km/h
Time taken is only 4 min `(4/60 "hr")` more than usual time
∴ time taken = `("t" + 1/35) "hr". (4/60 = 1/15)`
Using the formula,
`"Distance"/"Speed"` = time
Multiplying by 85 on both sides
`"d"/85 xx 85 = 85 xx "t" + 85 xx 1/15`
∴ d = `85"t" + 17/3` ...(2)
From (1) and (2), we will solve for ‘r’
Equating and eliminating ‘d’ we get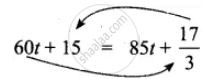
∴ By transposing, we get
`15 - 17/3` = 85t − 60t
`(45 - 17)/3` = 25t
∴ 25t = `28/3`
∴ t = `28/(3 xx 25)`
= `28/75` hr ...`(28/75 xx 60 = 22.4 "min")`
Substituting this value of ‘t’ in eqn. (1), we get
d = 60t + 15
= `60 xx 28/75 + 15`
= `1680/75 + 15`
= 22.4 + 15
= 37.4 km
APPEARS IN
RELATED QUESTIONS
x = 25 is the solution of one third of a number is less than 10 the original number.
How much smaller is 2ab + 4b – c than 5ab – 3b + 2c
Arivazhagan is 30 years younger to his father. Write Arivazhagan’s age in terms of his father’s age
The rectangles made of identical square blocks with varying lengths but having only two square blocks as width are given below
(i) How many small size squares are there in each of the rectangles P, Q, R and S?
(ii) Fill in the boxes
| Rectangle | P | Q | R | S | T |
| Number of small size squares along the breadth | 2 | 2 | ? | 2 | 2 |
| Number of squares along the length | 1 | 4 | 3 | ? | x |
| Total number of squares in rectangle | ? | 8 | ? | 10 | ? |
If the perimeter of a regular hexagon is x metres, then the length of each of its sides is ______.
If 7x + 4 = 25, then the value of x is ______.
2x – 5 > 11 is an equation.
In an equation, the LHS is equal to the RHS.
Write an equation whose solution is not a whole number.
Translate the following statements into an equation:
Amount (a) is equal to the sum of principal (p) and interest (i).
