Advertisements
Advertisements
प्रश्न
If the ice at the poles melts and flows towards the equator, how will it affect the duration of day-night?
उत्तर
Ice caps near the poles concentrate the mass of water at the poles through which axis of rotation of the Earth passes. If the ice melts, water will spread across the globe due to hydrostatic equilibrium and tend to move to the equatorial areas of the Earth due to centrifugal force of rotation. Mass, now being distributed more along the equator, will increase MI of the Earth and this in turn will decrease the angular velocity of the Earth. Decrease in angular velocity will increase the duration of day-night.
APPEARS IN
संबंधित प्रश्न
A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is __________ .
A closed cylindrical tube containing some water (not filling the entire tube) lies in a horizontal plane. If the tube is rotated about a perpendicular bisector, the moment of inertia of water about the axis __________ .
A cubical block of mass M and edge a slides down a rough inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has a magnitude
The centre of a wheel rolling on a plane surface moves with a speed \[\nu_0\] A particle on the rim of the wheel at the same level as the centre will be moving at speed ___________ .
A wheel of radius 20 cm is pushed to move it on a rough horizontal surface. If is found to move through a distance of 60 cm on the road during the time it completes one revolution about the centre. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is ______________________ .
A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of a smooth incline and released. Least time will be taken in reaching the bottom by _________ .
Consider a wheel of a bicycle rolling on a level road at a linear speed \[\nu_0\] (see the following figure)
(a) the speed of the particle A is zero
(b) the speed of B, C and D are all equal to \[v_0\]
(c) the speed of C is 2 \[v_0\]
(d) the speed of B is greater than the speed of O.

Three particles, each of mass 200 g, are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertial of the system about an axis joining two of the particles.

Particles of masses 1 g, 2 g, 3 g, .........., 100 g are kept at the marks 1 cm, 2 cm, 3 cm, ..........., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
The moment of inertia of a uniform rod of mass 0⋅50 kg and length 1 m is 0⋅10 kg-m2about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius. Find the distance of the line from the centre.
Find the moment of inertia of a uniform square plate of mass m and edge a about one of its diagonals.
Because of the friction between the water in oceans with the earth's surface the rotational kinetic energy of the earth is continuously decreasing. If the earth's angular speed decreases by 0⋅0016 rad/day in 100 years find the average torque of the friction on the earth. Radius of the earth is 6400 km and its mass is 6⋅0 × 1024 kg.
Suppose the rod in the previous problem has a mass of 1 kg distributed uniformly over its length.
(a) Find the initial angular acceleration of the rod.
(b) Find the tension in the supports to the blocks of mass 2 kg and 5 kg.
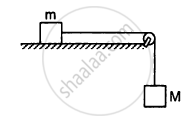
The following figure shows two blocks of mass m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
A small spherical ball is released from a point at a height h on a rough track shown in the following figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

