Advertisements
Advertisements
प्रश्न
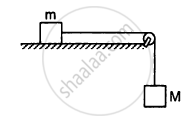
The following figure shows two blocks of mass m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
उत्तर
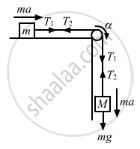
According to the equation, we have
\[Mg - T_1 = Ma ..........(1)\]
\[T_2 = ma ............(2)\]
\[ \Rightarrow \left( T_1 - T_2 \right) = \frac{Ia}{r^2}............(3)\left[\text{Because, }a = ra \right]\]
If we add the equations (1) and (2), we get
\[Mg + T_2 - T_1 = Ma + ma...........(4)\]
\[ \Rightarrow Mg - I\frac{a}{r^2} = Ma + ma\]
\[ \Rightarrow \left( M + m + \frac{I}{r^2} \right) a = Mg\]
\[ \Rightarrow a = \frac{Mg}{M + m + \frac{I}{r^2}}\]
APPEARS IN
संबंधित प्रश्न
If the ice at the poles melts and flows towards the equator, how will it affect the duration of day-night?
A hollow sphere, a solid sphere, a disc and a ring all having same mass and radius are rolled down on an inclined plane. If no slipping takes place, which one will take the smallest time to cover a given length?
A thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become
A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of a smooth incline and released. Least time will be taken in reaching the bottom by _________ .
A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top on an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by ___________ .
In the previous question, the smallest kinetic energy at
the bottom of the incline will be achieved by ___________ .
Consider a wheel of a bicycle rolling on a level road at a linear speed \[\nu_0\] (see the following figure)
(a) the speed of the particle A is zero
(b) the speed of B, C and D are all equal to \[v_0\]
(c) the speed of C is 2 \[v_0\]
(d) the speed of B is greater than the speed of O.

Three particles, each of mass 200 g, are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertial of the system about an axis joining two of the particles.

Particles of masses 1 g, 2 g, 3 g, .........., 100 g are kept at the marks 1 cm, 2 cm, 3 cm, ..........., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
The moment of inertia of a uniform rod of mass 0⋅50 kg and length 1 m is 0⋅10 kg-m2about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius. Find the distance of the line from the centre.
Because of the friction between the water in oceans with the earth's surface the rotational kinetic energy of the earth is continuously decreasing. If the earth's angular speed decreases by 0⋅0016 rad/day in 100 years find the average torque of the friction on the earth. Radius of the earth is 6400 km and its mass is 6⋅0 × 1024 kg.
Suppose the rod in the previous problem has a mass of 1 kg distributed uniformly over its length.
(a) Find the initial angular acceleration of the rod.
(b) Find the tension in the supports to the blocks of mass 2 kg and 5 kg.
A sphere of mass m rolls on a plane surface. Find its kinetic energy at an instant when its centre moves with speed \[\nu.\]
A small spherical ball is released from a point at a height h on a rough track shown in the following figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

