Advertisements
Advertisements
प्रश्न
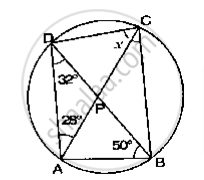
If O is the centre of the circle, find the value of x in the following figures.

उत्तर

∠BAO = ∠CDO = 52° (Angle in the same segment)
Δ DOC is an isosceles triangle
So, OD =OC (Radius of the same circle)
Then ∠ODC = ∠OCD = 52°
Hence X = 52°
APPEARS IN
संबंधित प्रश्न
Fill in the blank:
A circle divides the plane, on which it lies, in ............ parts.
If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure

If O is the centre of the circle, find the value of x in the following figure
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A
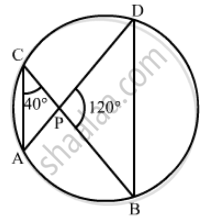
In the given figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.
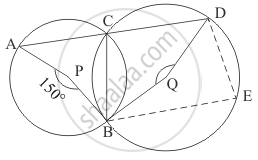
In the given figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

In the given figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.

In the given figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =