Advertisements
Advertisements
प्रश्न
In a cyclotron, magnetic field of 3·5Wb/m2 is used to accelerate protons. What should be the time interval in which the electric field between the Dees be reversed?
(Mass of proton = 1· 67 x 10-27Kg, Charge on proton =1·6x10-19c).
उत्तर
B = 3.5 Wb/m2 , mP = 1.67 × 10-27 Kg,
e = 1.6 × 10-19 C,
t = ?
t = `pi"m"_"P"/"Bq"_"p"`
t = `(3.142 xx 1.67 xx 10^-27)/(3.5 xx 1.6 xx 10^-19)`
`= (3.142 xx 1.67)/(3.5 xx 1.6) xx 10^-8`
= [log (3.142) + log (1.67) - log (3.5) - log (1.6)] × 10-8
= [0.4972 + 0.2227 - 0.5441 - 0.2041] × 10-8
= [antilog (- 0.0283)] × 10-8 s
= 0.9369 × 10-8 s
= 9.369 × 10-9 s
The dees should be reversed within time interval of 9.369 × 10-9 S.
APPEARS IN
संबंधित प्रश्न
Which one of the following particles cannot be accelerated by a cyclotron?
(A) Electrons
(B) Protons
(C) Deuterons
(D) α- particles
Show that the time period of revolution of particles in a cyclotron is independent of their speeds. Why is this property necessary for the operation of a cyclotron?
State the underlying principle of a cyclotron. Write briefly how this machine is used to accelerate charged particles to high energies
A proton and an electron travelling along parallel paths enter a region of uniform magnetic field, acting perpendicular to their paths. Which of them will move in a circular path with higher frequency?
An α-particle and a proton are released from the centre of the cyclotron and made to accelerate.
(i) Can both be accelerated at the same cyclotron frequency?
Give reason to justify your answer.
(ii) When they are accelerated in turn, which of the two will have higher velocity at the exit slit of the does?
Explain the principle and working of a cyclotron with the help of a schematic diagram. Write the expression for cyclotron frequency.
A cyclotron is used to accelerate protons to a kinetic energy of 5 MeV. If the strength of magnetic field in the cyclotron is 2T, find the radius and the frequency needed for the applied alternating voltage of the cyclotron. (Given : Velocity of proton= `3xx10^7 m//s`)
Which of the following particles will describe the smallest circle when projected with the same velocity perpendicular to a magnetic field?
If a charged particle kept at rest experiences an electromagnetic force,
(a) there must be an electric field
(b) there must be a magnetic field
(c) both fields cannot be zero
(d) both fields can be non-zero
An electron is projected horizontally with a kinetic energy of 10 keV. A magnetic field of strength 1.0 × 10−7 T exists in the vertically upward direction.
(a) Will the electron deflect towards the right or left of its motion?
(b) Calculate the sideways deflection of the electron while travelling through 1 m. Make appropriate approximations.
Figure shows a rod PQ of length 20.0 cm and mass 200 g suspended through a fixed point O by two threads of lengths 20.0 cm each. A magnetic field of strength 0.500 T exists in the vicinity of the wire PQ, as shown in the figure. The wires connecting PQ with the battery are loose and exert no force on PQ. (a) Find the tension in the threads when the switch S is open. (b) A current of 2.0 A is established when the switch S is closed. Find the tension in the threads now.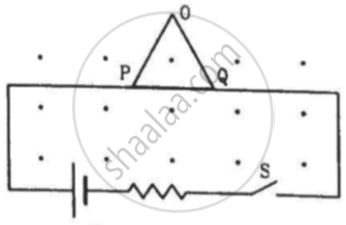
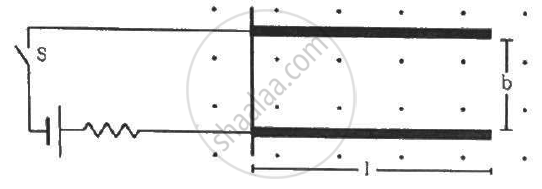
Two metal strips, each of length l, are clamped parallel to each other on a horizontal floor with a separation b between them. A wire of mass m lies on them perpendicularly, as shown in the figure. A vertically-upward magnetic field of strength B exists in the space. The metal strips are smooth but the coefficient of friction between the wire and the floor is µ. A current i is established when the switch S is closed at the instant t = 0. Discuss the motion of the wire after the switch is closed. How far away from the strips will the wire reach?
(a) An electron moves along a circle of radius 1 m in a perpendicular magnetic field of strength 0.50 T. What would be its speed? Is it reasonable? (b) If a proton moves along a circle of the same radius in the same magnetic field, what would be its speed?
\[\ce{Fe+}\] ions are accelerated through a potential difference of 500 V and are injected normally into a homogeneous magnetic field B of strength 20.0 mT. Find the radius of the circular paths followed by the isotopes with mass numbers 57 and 58. Take the mass of an ion = A (1.6 × 10−27) kg, where A is the mass number.
Answer the following question.
State the underlying principle of a cyclotron. Explain its working with the help of a schematic diagram. Obtain the expression for cyclotron frequency.
A cyclotron's oscillator frequency is 10 MHz. What should be the operating magnetic field for accelerating protons? If the radius of its 'dees' is 60 cm, calculate the kinetic energy (in MeV) of the proton beam produced by the accelerator.
Cyclotron frequency of a charged particle having charge q and mass m in a cyclotron producing magnetic field B is ______.
Assertion: The frequency of circular motion of a charged particle in cyclotron is independent of the mass of the particle.
Reason: Greater the mass of the particle less will be the frequency of the particle.
A charged particle is moving in a cyclotron, what effect on the radius of path of this charged particle will occur when the frequency of the ratio frequency field is doubled?
An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km/h. Its centripetal acceleration is ______.
The life time of muon in the rest frame is 2 × 10-6 sec. A beam of muons emerges from a cyclotron with velocity where c is the velocity of light The mean life of muons observed in the laboratory frame will be ______.
A cyclotron can accelerate ______.
In a cyclotron, a charged particle ______.
Describe the motion of a charged particle in a cyclotron if the frequency of the radio frequency (rf) field were doubled.
