Advertisements
Advertisements
प्रश्न
In fig., AB ⊥ BC and DC ⊥ BC, AB = 6, DC = 4 then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?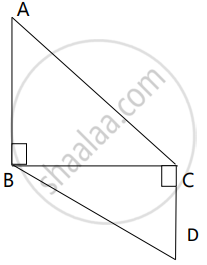
उत्तर
ΔABC and ΔBCD have same base BC.
∴ `"A(ΔABC)"/"A(ΔBCD)" = "AB"/"DC"` .....[Triangles having equal base]
∴ `"A(ΔABC)"/"A(ΔBCD)" = 6/4` .....[Given]
∴ `("A"(Δ"ABC"))/("A"(Δ"BCD")) = 3/2`
APPEARS IN
संबंधित प्रश्न
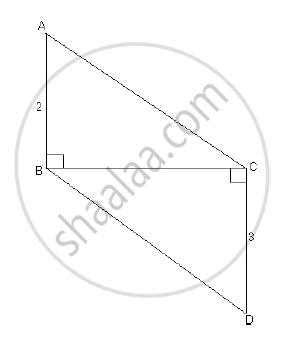
In the following figure seg AB ⊥ seg BC, seg DC ⊥ seg BC. If AB = 2 and DC = 3, find `(A(triangleABC))/(A(triangleDCB))`
The ratio of the areas of two triangles with the common base is 14 : 9. Height of the larger triangle is 7 cm, then find the corresponding height of the smaller triangle.
In the following figure RP: PK= 3:2, then find the value of A(ΔTRP):A(ΔTPK).

In the given figure, AD is the bisector of the exterior ∠A of ∆ABC. Seg AD intersects the side BC produced in D. Prove that :
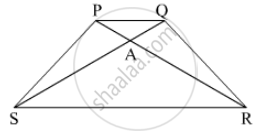
In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
In ∆ABC, B - D - C and BD = 7, BC = 20 then find following ratio.
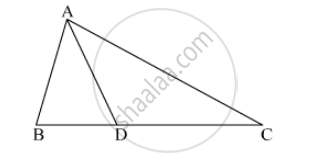
`"A(∆ ABD)"/"A(∆ ADC)"`
Ratio of areas of two triangles with equal heights is 2 : 3. If base of the smaller triangle is 6 cm then what is the corresponding base of the bigger triangle ?
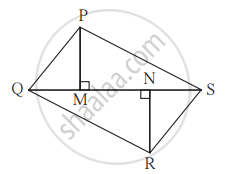
In the figure, PM = 10 cm, A(∆PQS) = 100 sq.cm, A(∆QRS) = 110 sq. cm, then find NR.
In ∆ABC, B – D – C and BD = 7, BC = 20, then find the following ratio.
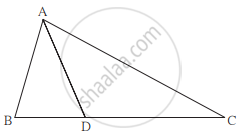
`(A(∆ABD))/(A(∆ABC))`
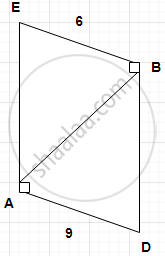
In the given, seg BE ⊥ seg AB and seg BA ⊥ seg AD.
if BE = 6 and AD = 9 find `(A(Δ ABE))/(A(Δ BAD))`.
A roller of diameter 0.9 m and the length 1.8 m is used to press the ground. Find the area of the ground pressed by it in 500 revolutions.
`(pi=3.14)`
Areas of two similar triangles are in the ratio 144: 49. Find the ratio of their corresponding sides.
Ratio of corresponding sides of two similar triangles is 4:7, then find the ratio of their areas = ?
In fig., PM = 10 cm, A(ΔPQS) = 100 sq.cm, A(ΔQRS) = 110 sq.cm, then NR?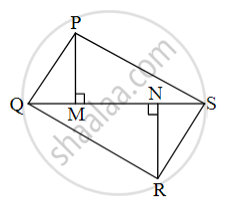
ΔPQS and ΔQRS having seg QS common base.
Areas of two triangles whose base is common are in proportion of their corresponding [______]
`("A"("PQS"))/("A"("QRS")) = (["______"])/"NR"`,
`100/110 = (["______"])/"NR"`,
NR = [ ______ ] cm
If ΔABC ∼ ΔDEF, length of side AB is 9 cm and length of side DE is 12 cm, then find the ratio of their corresponding areas.
In the figure, PQ ⊥ BC, AD ⊥ BC. To find the ratio of A(ΔPQB) and A(ΔPBC), complete the following activity.
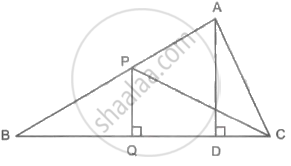
Given: PQ ⊥ BC, AD ⊥ BC
Now, A(ΔPQB) = `1/2 xx square xx square`
A(ΔPBC) = `1/2 xx square xx square`
Therefore,
`(A(ΔPQB))/(A(ΔPBC)) = (1/2 xx square xx square)/(1/2 xx square xx square)`
= `square/square`
