Advertisements
Advertisements
प्रश्न
In Figure 3, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm have been drawn, with centres A,B, C and D, then find the area of the shaded region.

उत्तर
Here,
Radii of the arcs with centres A, B, C and D = 7 cm
And,
AB = 18 cm
DC = 32 cm
Distance between AB and DC = 14 cm
Area of trapezium ABCD = \[\frac{1}{2}\left( 18 + 32 \right)14\]
= 350 cm2
Now,
Area of unshaded region = Area of sector with central ∠∠A + Area of sector with central ∠∠B + Area of sector with central ∠∠C + Area of sector with central ∠∠D
\[= \frac{\angle A}{360^o} \times \pi \times \left( 7 \right)^2 + \frac{\angle B}{360^o} \times \pi \times \left( 7 \right)^2 + \frac{\angle C}{360^o} \times \pi \times \left( 7 \right)^2 + \frac{\angle D}{360^o} \times \pi \times \left( 7 \right)^2 \]
\[ = \pi \times \left( 7 \right)^2 \left( \frac{\angle A}{360^o} + \frac{\angle B}{360^o} + \frac{\angle C}{360^o} + \frac{\angle D}{360^o} \right)\]
\[ = \frac{22}{7} \times \left( 7 \right)^2 \left( \frac{\angle A + \angle B + \angle C + \angle D}{360^o} \right)\]
\[ = 154\left( \frac{360^o}{360^O} \right) \left( \text{Angle sum property of quadrilateral} \right)\]
\[ = 154 {cm}^2\]
∴ Area of the shaded region = Area of trapezium ABCD − Area of unshaded region
= 350 − 154
= 196 cm2
APPEARS IN
संबंधित प्रश्न
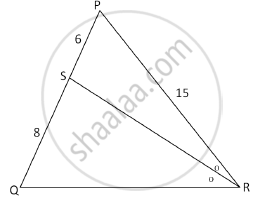
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In figure, find ∠L

D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle
Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

- ΔADE ∼ ΔACB.
- If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
- Find, area of ΔADE : area of quadrilateral BCED.
In triangle ABC, DE is parallel to BC; where D and E are the points on AB and AC respectively.
Prove: ∆ADE ~ ∆ABC.
Also, find the length of DE, if AD = 12 cm, BD = 24 cm BC = 8 cm.
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
The given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate:
- the length of AP,
- the ratio of the areas of triangle APQ and triangle ABC.
In the given figure, triangle ABC is similar to triangle PQR. AM and PN are altitudes whereas AX and PY are medians.
prove that
`("AM")/("PN")=("AX")/("PY")`
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
The length of a river in a map is 54cm. if lcm on the map represents 12500m on land, find the length of the river.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of AB, if A' B' = 6 cm.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
In the following figure, M is mid-point of BC of a parallelogram ABCD. DM intersects the diagonal AC at P and AB produced at E. Prove that : PE = 2 PD

In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
ΔABC is enlarged, with a scale factor 5. Find: BC, f B'C' = 16cm
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The number of KM represented by 2cm on the map.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
On a map drawn to a scale of 1:25000, a triangular plot of land is right angled and the sides forming the right angle measure 225cm and 64cm.Find: The area of the plot in sq. km.
In the adjacent figure, ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm and AP = 2.8 cm, find CA and AQ

If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.

ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
